Introduction
The Global Historical Climatology Network daily (GHCNd) is an integrated database of daily climate summaries from land surface stations across the globe. GHCNd is made up of daily climate records from numerous sources that have been integrated and subjected to a common suite of quality assurance reviews.
GHCNd contains records from more than 100,000 stations in 180 countries and territories. NCEI provides numerous daily variables, including maximum and minimum temperature, total daily precipitation, snowfall, and snow depth. About half the stations only report precipitation. Both record length and period of record vary by station and cover intervals ranging from less than a year to more than 175 years. - noaa.gov
The question I have been investigating is whether the maximum temperature of a day is exhibiting a trend over the years.
The objective followed in the notebook that lead to this post is to explore a series of Bayesian models that relate the maximum daily temperature with time and see what trends we can find. This is a bunch of Bayesian regression models. We will use the PyMC library to do the Bayesian inference.
Setup
The following is based on a Jupyter notebook converted to Markdown.
Imports
import pandas as pd
from tqdm.auto import tqdm
import os
import glob
import numpy as np
from multiprocessing import Pool
import polars as pl
import importlib
import re
import gc
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from matplotlib import colors
import matplotlib as mpl
import statsmodels.api as sm
import statsmodels.graphics.gofplots as gofplots
import pymc as pm
import arviz as az
import geopandas as gpd
import folium
from folium.features import GeoJsonTooltip
from shapely.geometry import Polygon, LineString, Point
%config InlineBackend.figure_format = 'retina'
# disable future warnings
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
sns.set_style("darkgrid")
pl.enable_string_cache()!dateMon Oct 30 17:10:07 UTC 2023Parameters
# the first year of data to use
start_year = 2010
# the list of counties to use - FIPS codes
counties = [6085]
# The minimum number of days of data of valid data for a station not to be dropped
MIN_DAYS_OF_DATA = 2 * 365
# Sampling parameters
# Whether to compute convergence checks
compute_convergence_checks = True
# Whether to compute the posterior predictive
sample_posterior_predictive = True
# Whether to compute the log likelihood
compute_log_likelihood = True
# The sampler to use
nuts_sampler='pymc'
# something to identify the run
nonce = "na"print("Start year: ", start_year)
print("Counties: ", counties)
print("Convergence checks: ", compute_convergence_checks)
print("Sample posterior predictive: ", sample_posterior_predictive)
print("Compute log likelihood: ", compute_log_likelihood)
print("NUTS sampler: ", nuts_sampler)
print("Nonce: ", nonce)Start year: 2010
Counties: [6085]
Convergence checks: True
Sample posterior predictive: True
Compute log likelihood: True
NUTS sampler: pymc
Nonce: naLibrary
Build, install and load the library of tools.
!cd ../crates/py_analysis ; maturin develop -q --release🍹 Building a mixed python/rust project
🔗 Found pyo3 bindings
🐍 Found CPython 3.10 at /opt/conda/bin/python
📡 Using build options features from pyproject.toml
📦 Built wheel for CPython 3.10 to /tmp/.tmpEnBPOp/py_analysis-0.1.0-cp310-cp310-linux_x86_64.whl
🛠 Installed py_analysis-0.1.0import py_analysis as pa
importlib.reload(pa.load)
importlib.reload(pa.display)
importlib.reload(pa.ghcn_d)
importlib.reload(pa.utils)
importlib.reload(pa)Data
Geojson of US counties:
geojson = pa.load_county_parquet('../data/georef-united-states-of-america-county.parquet')
geojson.head()| coty_code | geometry | coty_name | ste_name | |
|---|---|---|---|---|
| 0 | 29063 | POLYGON ((-94.60226 39.74719, -94.59837 39.747… | DeKalb | Missouri |
| 1 | 29101 | POLYGON ((-94.06432 38.56738, -94.05580 38.567… | Johnson | Missouri |
| 2 | 29115 | POLYGON ((-93.36196 39.96761, -93.36136 39.967… | Linn | Missouri |
| 3 | 29121 | POLYGON ((-92.69215 39.61026, -92.68930 39.610… | Macon | Missouri |
| 4 | 29510 | POLYGON ((-90.18123 38.66007, -90.18260 38.665… | St. Louis | Missouri |
Get NOAA GHCN daily data (https://docs.opendata.aws/noaa-ghcn-pds/readme.html) and convert to parquet. You can be smarter and get the parquet files directly…
pa.ghcn_d.download_all_until(2022, directory="../data/ghcn_d/")
_ = pa.ghcn_d.ghcn_d_csv_to_parquet(verbose=True, files="../data/ghcn_d/*.csv.gz")Available years: [1763, 1764, 1765, 1766, 1767, [...] 2019, 2020, 2021, 2022]
Doneall_df = pl.scan_parquet('../data/ghcn_d/*.parquet').\
filter(pl.col('date').dt.year() >= start_year)Let’s see what the data looks like.
all_df.fetch()| station | date | element | value | m-flag | q-flag | s-flag | obs_time |
|---|---|---|---|---|---|---|---|
| str | date | cat | f32 | cat | cat | cat | time |
From NOAA GHCN-D README:
The yearly files are formatted so that every observation is represented by a single row with the following fields:
- ID = 11 character station identification code. Please see ghcnd-stations section below for an explantation
- YEAR/MONTH/DAY = 8 character date in YYYYMMDD format (e.g. 19860529 = May 29, 1986)
- ELEMENT = 4 character indicator of element type
- DATA VALUE = 5 character data value for ELEMENT
- M-FLAG = 1 character Measurement Flag
- Q-FLAG = 1 character Quality Flag
- S-FLAG = 1 character Source Flag
- OBS-TIME = 4-character time of observation in hour-minute format (i.e. 0700 =7:00 am)
The five core elements are:
- PRCP = Precipitation (tenths of mm)
- SNOW = Snowfall (mm)
- SNWD = Snow depth (mm)
- TMAX = Maximum temperature (tenths of degrees C)
- TMIN = Minimum temperature (tenths of degrees C)
M-FLAG is the measurement flag. Q-FLAG is the measurement quality flag. There are fourteen possible values:
- Blank = did not fail any quality assurance check
- D = failed duplicate check
- G = failed gap check
- I = failed internal consistency check
- K = failed streak/frequent-value check
- L = failed check on length of multiday period
- M = failed mega consistency check
- N = failed naught check
- O = failed climatological outlier check
- R = failed lagged range check
- S = failed spatial consistency check
- T = failed temporal consistency check
- W = temperature too warm for snow
- X = failed bounds check
- Z = flagged as a result of an official Datzilla Investigation
S-FLAG is the source flag for the observation.
And for the stations we have:
stations_df = pa.ghcn_d.load_stations(file="../data/stations_data.csv")
stations_df| station | name | state | latitude | longitude | elevation | county |
|---|---|---|---|---|---|---|
| str | str | str | f64 | f64 | f64 | i32 |
| "MXN00002073" | "TIJUANA (CFE)" | null | 32.5167 | -117.0667 | 25.0 | null |
| "MXN00002145" | "RANCHO WILLIAM… | null | 32.6167 | -114.8667 | 29.0 | null |
| "MXN00002101" | "EL CENTINELA" | null | 32.5667 | -115.7333 | 50.0 | null |
| "MXN00002078" | "RANCHO P. P. C… | null | 32.5667 | -116.65 | 559.9 | null |
| "MXN00002037" | "PRESA MORELOS" | null | 32.7 | -114.7167 | 39.9 | 4027 |
| "MXN00002070" | "VALLE REDONDO" | null | 32.5167 | -116.75 | 241.7 | null |
| "MXN00002086" | "EJIDO JACUME" | null | 32.5833 | -116.1833 | 859.8 | null |
| "MXN00002003" | "BATAQUEZ" | null | 32.55 | -115.0667 | 22.9 | null |
| "MXN00002136" | "AGUA HECHICERA… | null | 32.5333 | -116.6167 | 1164.9 | null |
| "MXN00002033" | "MEXICALI (DGE)… | null | 32.65 | -115.4667 | 2.7 | null |
| "MXN00002034" | "MEXICALI (SMN)… | null | 32.55 | -115.4667 | 2.7 | null |
| "MXN00002134" | "EJIDO CUERNAVA… | null | 32.55 | -115.3 | 7.9 | null |
| … | … | … | … | … | … | … |
| "USC00451830" | "CRESCENT" | "WA" | 47.75 | -117.9167 | 670.6 | 53043 |
| "USC00456789" | "PULLMAN 2 NW" | "WA" | 46.7603 | -117.1861 | 766.6 | 53075 |
| "USS0021A32S" | "Elbow Lake" | "WA" | 48.69 | -121.91 | 926.6 | 53073 |
| "USR0000WBRO" | "BROWN MTN. ORC… | "WA" | 48.5353 | -118.6889 | 990.6 | 53019 |
| "USS0021C41S" | "Cayuse Pass" | "WA" | 46.87 | -121.53 | 1597.2 | 53053 |
| "US1WAKG0253" | "RENTON 2.7 NE" | "WA" | 47.5132 | -122.1631 | 135.9 | 53033 |
| "US1WAKG0030" | "SHORELINE 1.0 … | "WA" | 47.7533 | -122.3254 | 143.9 | 53033 |
| "US1WACW0006" | "WOODLAND 3.5 N… | "WA" | 45.9583 | -122.7797 | 167.9 | 53015 |
| "US1WABT0015" | "RICHLAND 3.4 S… | "WA" | 46.2506 | -119.3243 | 175.9 | 53005 |
| "US1WACK0060" | "CAMAS 4.3 NNE" | "WA" | 45.645 | -122.3887 | 199.9 | 53011 |
| "US1WAKG0049" | "NEWPORT HILLS … | "WA" | 47.5465 | -122.1435 | 199.9 | 53033 |
| "US1WACK0026" | "CAMAS 1.0 NNW" | "WA" | 45.601 | -122.431 | 207.9 | 53011 |
Stations in the counties
# stations with data in the counties
q = stations_df.lazy()\
.filter(pl.col('county').is_in(counties))\
.join(all_df.filter(pl.col('element') == 'TMAX')\
.group_by(pl.col('station')).agg(
[pl.col('station').count().alias('count'),
pl.col('q-flag').is_not_null().count().alias('null_q'),
pl.col('date').min().alias('min_date'),
pl.col('date').max().alias('max_date')]),
on='station',
how='left')\
.filter(pl.col('count').is_not_null())\
.sort('count', descending=True)\
.lazy()
# q.show_graph()
counties_stations_df = q.collect()
counties_stations_df| station | name | state | latitude | longitude | elevation | county | count | null_q | min_date | max_date |
|---|---|---|---|---|---|---|---|---|---|---|
| str | str | str | f64 | f64 | f64 | i32 | u32 | u32 | date | date |
| "USW00023293" | "SAN JOSE" | "CA" | 37.3594 | -121.9244 | 14.9 | 6085 | 4600 | 4600 | 2010-01-01 | 2022-09-06 |
| "USC00045933" | "MT HAMILTON" | "CA" | 37.3433 | -121.6347 | 1286.3 | 6085 | 4592 | 4592 | 2010-01-01 | 2022-09-05 |
| "USC00048273" | "SKYLINE RIDGE … | "CA" | 37.3133 | -122.185 | 691.9 | 6085 | 4416 | 4416 | 2010-01-01 | 2022-08-31 |
| "USR0000CALT" | "LOS ALTOS CALI… | "CA" | 37.3581 | -122.1472 | 196.6 | 6085 | 4119 | 4119 | 2010-01-01 | 2021-04-25 |
| "USR0000CLGA" | "LOS GATOS CALI… | "CA" | 37.2028 | -121.9428 | 609.6 | 6085 | 4101 | 4101 | 2010-01-01 | 2021-04-25 |
| "USW00023244" | "MOFFETT FED AI… | "CA" | 37.4058 | -122.0481 | 11.9 | 6085 | 3478 | 3478 | 2010-01-01 | 2019-09-08 |
| "USC00043417" | "GILROY" | "CA" | 37.0031 | -121.5608 | 59.1 | 6085 | 3372 | 3372 | 2010-01-01 | 2022-09-06 |
| "USR0000CPOV" | "POVERTY CALIFO… | "CA" | 37.4431 | -121.7706 | 629.7 | 6085 | 3278 | 3278 | 2010-01-01 | 2021-04-25 |
| "USC00046646" | "PALO ALTO" | "CA" | 37.4436 | -122.1403 | 7.6 | 6085 | 2566 | 2566 | 2010-01-02 | 2017-12-30 |
| "USC00045123" | "LOS GATOS" | "CA" | 37.2319 | -121.9592 | 111.3 | 6085 | 2361 | 2361 | 2010-01-01 | 2019-01-28 |
def markers_fn(us_map):
return stations_df.filter(pl.col('county').is_in(counties)).to_pandas().apply(
lambda row:folium.CircleMarker(location=[row['latitude'], row['longitude']],
radius=1,
hue='red',
fill=True).add_to(us_map),
axis=1)
pa.plot_county_geojson(geojson, counties, zoom_start=8, markers_fn=markers_fn)There are many stations but not all have data or valid data or valid and recent data. Let’s see what we have.
Activity of stations
We will only use the data where the quality flag is null.
# stations with data in the counties and no q-flag
q = stations_df.lazy() \
.filter(pl.col('county').is_in(counties)) \
.join(all_df.filter(pl.col('element') == 'TMAX') \
.filter(pl.col('q-flag').is_null()) \
.group_by(pl.col('station')).agg(pl.col('date')),
on='station',
how='left') \
.filter(pl.col('date').is_not_null())\
.group_by(pl.col('station')).agg(pl.col('date').explode().alias('dates'))
counties_stations_activity_df = q.collect()
counties_stations_activity_df| station | dates |
|---|---|
| str | list[date] |
| "USW00023293" | [2010-01-01, 2010-01-02, … 2022-09-06] |
| "USW00023244" | [2010-01-01, 2010-01-02, … 2019-09-08] |
| "USC00048273" | [2010-01-01, 2010-01-02, … 2022-08-31] |
| "USC00045933" | [2010-01-01, 2010-01-02, … 2022-09-05] |
| "USR0000CLGA" | [2010-01-01, 2010-01-02, … 2021-04-25] |
| "USC00046646" | [2010-01-02, 2010-01-03, … 2017-12-30] |
| "USC00043417" | [2010-01-01, 2010-01-02, … 2022-09-06] |
| "USC00045123" | [2010-01-01, 2010-01-02, … 2019-01-28] |
| "USR0000CPOV" | [2010-01-01, 2010-01-02, … 2021-04-25] |
| "USR0000CALT" | [2010-01-01, 2010-01-02, … 2021-04-25] |
Let’s visualize when these stations have been reporting (valid) data.
def format_station_name(station_id, stations_df=stations_df, new_line=True):
"""
Format the name of a station given its id.
"""
station = stations_df.row(by_predicate=(pl.col('station') == station_id), named=True)
if new_line:
return f"{station['name']}\n{station_id}"
else:
return f"{station['name']} - {station_id}"# heatmap with a row for each station and a column for each day
counties_stations_heatmap = counties_stations_activity_df.with_columns(pl.lit(1).alias('something'))\
.explode('dates')\
.rename({'dates': 'date'})\
.pivot(index='date', columns=['station'], values='something')\
.sort('date')\
.fill_null(0)\
.upsample(time_column='date', every='1d')\
.sort('date')
# plot the heatmap with seaborn
fig, ax = plt.subplots(figsize=(20, 10))
sns.heatmap(counties_stations_heatmap.to_pandas().set_index('date').T,
ax=ax, cbar=False, cmap='Blues', xticklabels="auto", yticklabels="auto")
ax.set_xlabel('Date')
ax.set_ylabel('Station')
ax.set_title('County Stations Activity')
# only show the year on the x-axis
# ax.xaxis.set_major_locator(mdates.YearLocator())
ax.set_xticklabels([item.get_text()[:4] for item in ax.xaxis.get_ticklabels()])
# ylabel with station id and name
ax.set_yticklabels([format_station_name(item.get_text()) for item in ax.yaxis.get_ticklabels()])
del counties_stations_activity_df
plt.show()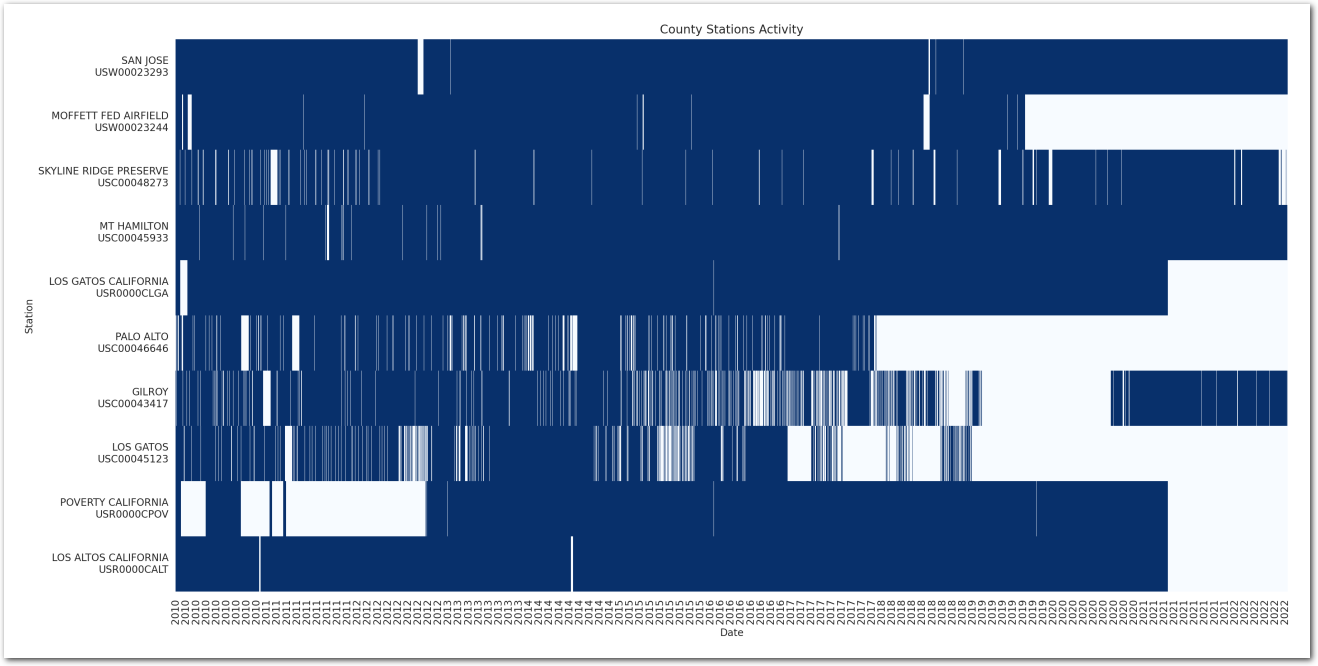
Remove stations with almost no data - we are interested in estimating the trends and we need enough data to do that:
stations_to_ignore = counties_stations_df.filter(pl.col('null_q') < MIN_DAYS_OF_DATA).select('station', 'null_q', 'min_date', 'max_date')
stations_to_ignoreThey are no such station in this run.
| station | null_q | min_date | max_date |
|---|---|---|---|
| str | u32 | date | date |
TMAX over the years
In the following, we focus on the maximum intraday temperature - ‘TMAX’. And want to know how it has changed over time. We suspect that ‘data’ of the measure is a factor, but also the time of the year (season) that we will capture through the ‘month’ of the measure and the ‘station’ where it has been measured too.
q = stations_df.lazy()\
.filter(pl.col('county').is_in(counties))\
.filter(pl.col('station').is_in(list(stations_to_ignore['station'])).not_())\
.join(all_df.filter(pl.col('element').is_in(['TMAX', 'TMIN']) & pl.col("q-flag").is_null())\
.select([pl.col('station'), pl.col('element'), pl.col('date'), pl.col('value')]),
on='station',
how='inner')\
.with_columns([
pl.col('station').cast(pl.Categorical),
pl.col('state').cast(pl.Categorical),
pl.col('name').cast(pl.Categorical),
pl.col('date').cast(pl.Date)
]) \
.sort(['date', 'station', 'element'], descending=True) \
.lazy()
wx_df = q.collect().pivot(index=['date', 'station', 'state', 'name', 'latitude', 'longitude', 'elevation', 'county'], columns='element', values='value')
print(f"wx_df.shape: {wx_df.shape}")
wx_df.head()wx_df.shape: (36895, 10)| date | station | state | name | latitude | longitude | elevation | county | TMIN | TMAX |
|---|---|---|---|---|---|---|---|---|---|
| date | cat | cat | cat | f64 | f64 | f64 | i32 | f32 | f32 |
| 2022-09-06 | "USW00023293" | "CA" | "SAN JOSE" | 37.3594 | -121.9244 | 14.9 | 6085 | 23.299999 | 42.799999 |
| 2022-09-06 | "USC00043417" | "CA" | "GILROY" | 37.0031 | -121.5608 | 59.1 | 6085 | 21.1 | 45.0 |
| 2022-09-05 | "USW00023293" | "CA" | "SAN JOSE" | 37.3594 | -121.9244 | 14.9 | 6085 | 20.0 | 40.0 |
| 2022-09-05 | "USC00045933" | "CA" | "MT HAMILTON" | 37.3433 | -121.6347 | 1286.3 | 6085 | 28.299999 | 35.599998 |
| 2022-09-05 | "USC00043417" | "CA" | "GILROY" | 37.0031 | -121.5608 | 59.1 | 6085 | 20.0 | 44.400002 |
# dataframe with the data as index and a column for each station - each cell is the value of the station for that day
wx_df_pivot = wx_df.to_pandas().pivot(index='date', columns='station', values='TMAX')
# fill missing dates
wx_df_pivot = wx_df_pivot.asfreq('D', fill_value=np.nan)
# convert to int
wx_df_pivot = wx_df_pivot.astype(float)
# plot the heatmap with seaborn
fig, ax = plt.subplots(figsize=(20, 10))
sns.heatmap(wx_df_pivot.T,
ax=ax, cbar=True,
cmap='coolwarm', xticklabels="auto", yticklabels="auto")
ax.set_xlabel('Station')
ax.set_ylabel('Date')
ax.set_title('Stations Activity')
# background color to see missing data
ax.set_facecolor('lightyellow')
ax.set_xticklabels([item.get_text()[:4] for item in ax.xaxis.get_ticklabels()])
# yticklabel with station name
ax.set_yticklabels([format_station_name(item.get_text()) for item in ax.yaxis.get_ticklabels()])
# reduce the size of the yticklabels
plt.yticks(fontsize=8)
plt.title('Stations TMAX')
del wx_df_pivot
plt.show()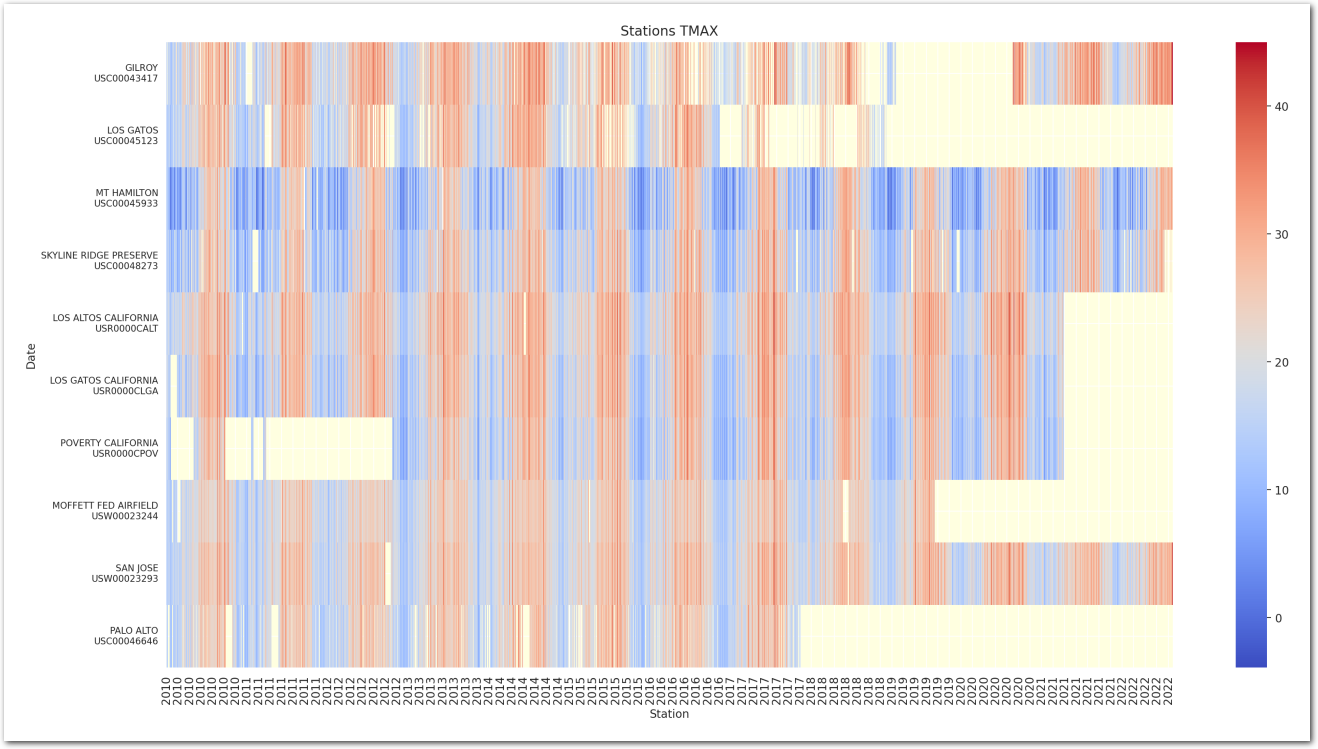
Let’s look at the time series of TMAX for the stations in the counties
plt.figure(figsize=(20, 10))
sns.scatterplot(data=wx_df.to_pandas(), x='date', y='TMAX', hue='station', alpha=0.5, s=10)
# legend on two columns
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0., ncol=2)
plt.title('Stations TMAX')
# keep the color map
handles, labels = plt.gca().get_legend_handles_labels()
station_cmap = {}
for h, l in zip(handles, labels):
station_cmap[l] = h.get_color()
plt.show()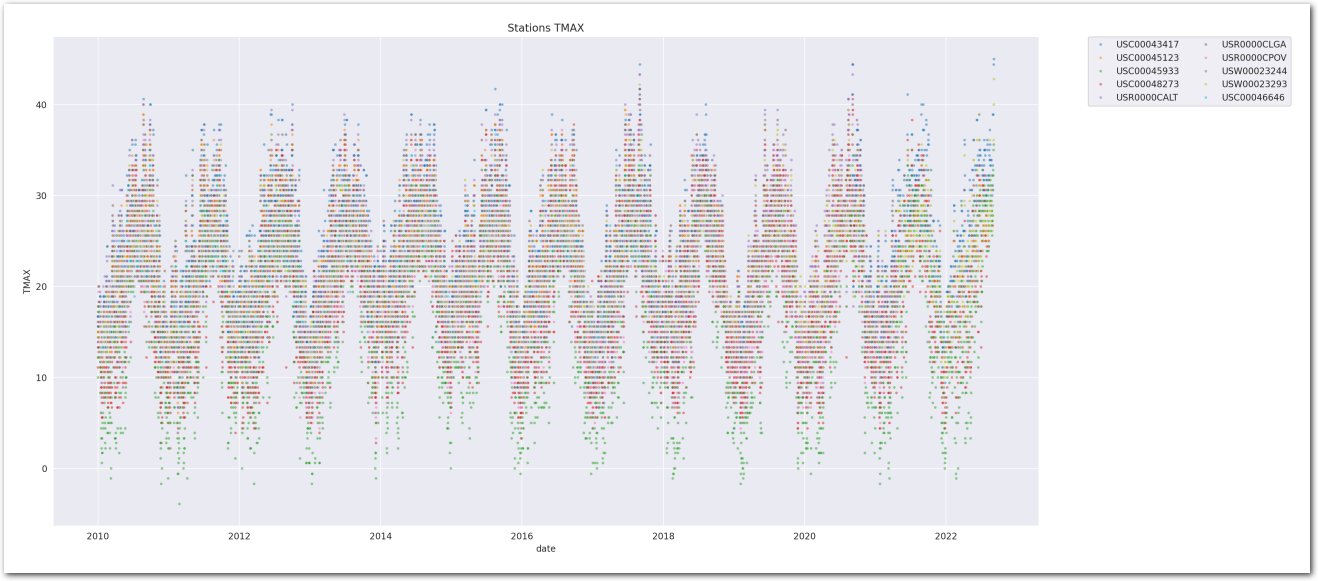
TMAX is reported in tenths of degrees C. This explains the weird pattern on the y-axis.
Let’s plot the same data as lineplots and on separate subplots:
# grid of plots with a plot for each station
g = sns.FacetGrid(wx_df.to_pandas(), row="station", hue="station", aspect=5, height=1, palette=station_cmap, sharex=True)
g.map(sns.lineplot, "date", "TMAX", alpha=0.9, linewidth=0.5, zorder=100)
g.set_titles("{row_name}")
g.add_legend()
# g.fig.subplots_adjust(hspace=0.5)
g.fig.set_size_inches(10, 20)
plt.show()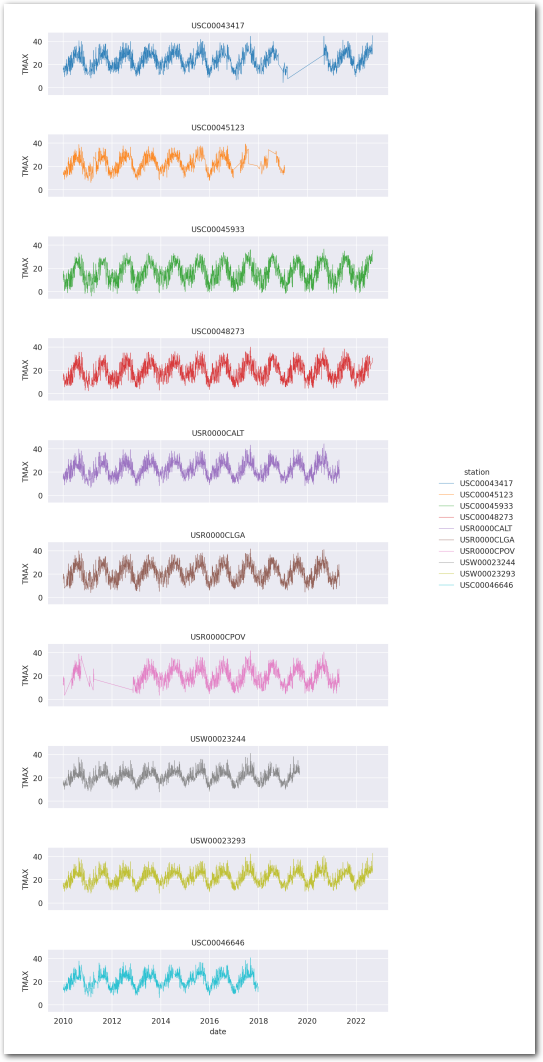
Variations within years
Let’s have a look at the variations within each year:
wx_df_plus = wx_df.with_columns([
pl.col('date').dt.year().alias('year'),
pl.col('date').dt.month().alias('month'),
pl.col('date').dt.ordinal_day().alias('day_of_year')])
print(f"wx_df_plus.shape: {wx_df_plus.shape}")
del wx_df
wx_df_plus.head()wx_df_plus.shape: (36895, 13)| date | station | state | name | latitude | longitude | elevation | county | TMIN | TMAX | year | month | day_of_year |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| date | cat | cat | cat | f64 | f64 | f64 | i32 | f32 | f32 | i32 | u32 | u32 |
| 2022-09-06 | "USW00023293" | "CA" | "SAN JOSE" | 37.3594 | -121.9244 | 14.9 | 6085 | 23.299999 | 42.799999 | 2022 | 9 | 249 |
| 2022-09-06 | "USC00043417" | "CA" | "GILROY" | 37.0031 | -121.5608 | 59.1 | 6085 | 21.1 | 45.0 | 2022 | 9 | 249 |
| 2022-09-05 | "USW00023293" | "CA" | "SAN JOSE" | 37.3594 | -121.9244 | 14.9 | 6085 | 20.0 | 40.0 | 2022 | 9 | 248 |
| 2022-09-05 | "USC00045933" | "CA" | "MT HAMILTON" | 37.3433 | -121.6347 | 1286.3 | 6085 | 28.299999 | 35.599998 | 2022 | 9 | 248 |
| 2022-09-05 | "USC00043417" | "CA" | "GILROY" | 37.0031 | -121.5608 | 59.1 | 6085 | 20.0 | 44.400002 | 2022 | 9 | 248 |
wx_pd = wx_df_plus.to_pandas()
plt.figure(figsize=(20, 10))
# add year and day_of_year columns
sns.scatterplot(data=wx_pd.reset_index(), x='day_of_year', y='TMAX', hue='year', style="station",
alpha=0.5, palette='RdBu_r', s=20)
# legend on two columns
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0., ncol=2)
ax = plt.gca()
ax.xaxis.set_major_locator(mdates.MonthLocator())
ax.xaxis.set_major_formatter(mdates.DateFormatter('%b'))
plt.title('Stations TMAX')
plt.show()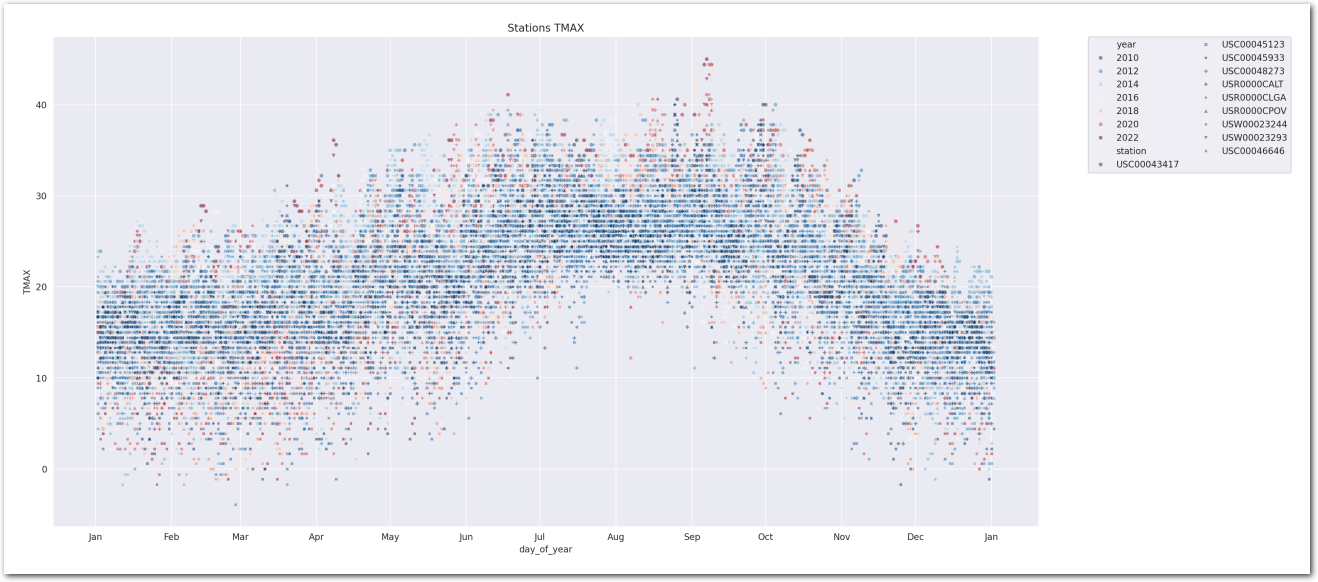
Monthly average of daily TMAX over the years
Let’s look at the variations from year to year of monthly average.
wx_df_plus_ = wx_df_plus.to_pandas()
wx_df_plus_ = wx_df_plus_.groupby([wx_df_plus_.date.dt.to_period('M'), 'station']).agg({'TMAX': ['mean', 'count']}).reset_index()
# filter out (stations, year) with less 20 points - per month
wx_df_plus_ = wx_df_plus_[wx_df_plus_[('TMAX', 'count')] > 20]
# remove multiindex
wx_df_plus_.columns = [' '.join(col).strip() for col in wx_df_plus_.columns.values]
# rename columns
wx_df_plus_.rename(columns={'TMAX count': 'count', 'TMAX mean': 'TMAX'}, inplace=True)
# drop year column
wx_df_plus_.drop(columns=['count'], inplace=True)
wx_df_plus_['date'] = wx_df_plus_['date'].astype('datetime64[ns]')
wx_df_plus_.head()| date | station | TMAX | |
|---|---|---|---|
| 0 | 2010-01-01 | USC00043417 | 15.400001 |
| 1 | 2010-01-01 | USC00045123 | 14.016129 |
| 2 | 2010-01-01 | USC00045933 | 9.045161 |
| 3 | 2010-01-01 | USC00048273 | 11.396552 |
| 4 | 2010-01-01 | USR0000CALT | 15.716129 |
fig = plt.figure(figsize=(20, 10))
# add year and day_of_year columns
sns.scatterplot(wx_df_plus_, x='date', y='TMAX', hue='station',
alpha=0.5, palette=station_cmap, s=50)
# legend on two columns
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0., ncol=2)
# format the x-axis - automatic
fig.autofmt_xdate()
plt.title('Stations TMAX by Month')
plt.show()
del wx_df_plus_
del wx_df_plus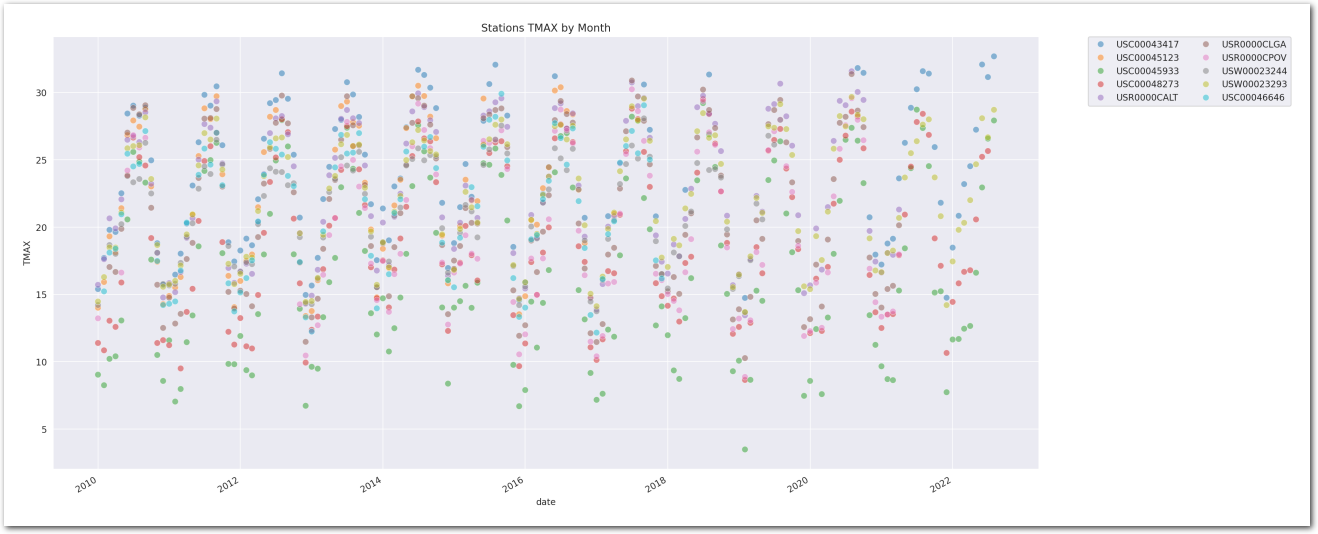
It’s hard to be definitive on a trend by visualizing this chart, though this seems to be trending upwards. Let’s build some models to estimate the trend.
Trends in TMAX
First we prepare the data for the models.
Data preparation
# remove rows with missing data for TMAX
wx_pd.dropna(subset=['TMAX'], inplace=True)
wx_pd.sort_values(['date', 'station'], inplace=True)
wx_pd.set_index(['date', 'station'], inplace=True)
print(f"wx_pd.shape: {wx_pd.shape}")
wx_pd.head()wx_pd.shape: (36839, 11)| state | name | latitude | longitude | elevation | county | TMIN | TMAX | year | month | day_of_year | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| date | station | |||||||||||
| 2010-01-01 | USC00043417 | CA | GILROY | 37.0031 | -121.5608 | 59.1 | 6085 | 7.2 | 16.700001 | 2010 | 1 | 1 |
| USC00045123 | CA | LOS GATOS | 37.2319 | -121.9592 | 111.3 | 6085 | 7.8 | 15.000000 | 2010 | 1 | 1 | |
| USC00045933 | CA | MT HAMILTON | 37.3433 | -121.6347 | 1286.3 | 6085 | 2.8 | 10.000000 | 2010 | 1 | 1 | |
| USC00048273 | CA | SKYLINE RIDGE PRESERVE | 37.3133 | -122.1850 | 691.9 | 6085 | 6.1 | 11.100000 | 2010 | 1 | 1 | |
| USR0000CALT | CA | LOS ALTOS CALIFORNIA | 37.3581 | -122.1472 | 196.6 | 6085 | 9.4 | 16.700001 | 2010 | 1 | 1 |
Build the index for the stations to parameterize the model:
station_idxs, stations = pd.factorize(wx_pd.index.get_level_values(1))
print(f"Number of stations: {len(stations)}")
print(f"Number of station_idxs: {len(station_idxs)}")
stationsNumber of stations: 10
Number of station_idxs: 36839
CategoricalIndex(['USC00043417', 'USC00045123', 'USC00045933', 'USC00048273',
'USR0000CALT', 'USR0000CLGA', 'USR0000CPOV', 'USW00023244',
'USW00023293', 'USC00046646'],
...)Same for the time:
time_idxs, times = pd.factorize(wx_pd.index.get_level_values(0))
print(f"Number of times: {len(times)}")
print(f"Number of time_idxs: {len(time_idxs)}")
timesNumber of times: 4632
Number of time_idxs: 36839
DatetimeIndex(['2010-01-01', '2010-01-02', '2010-01-03', '2010-01-04',
'2010-01-05', '2010-01-06', '2010-01-07', '2010-01-08',
'2010-01-09', '2010-01-10',
...
'2022-08-28', '2022-08-29', '2022-08-30', '2022-08-31',
'2022-09-01', '2022-09-02', '2022-09-03', '2022-09-04',
'2022-09-05', '2022-09-06'],
dtype='datetime64[ms]', length=4632, freq=None)Convert the time to a float in years. 0. is Epoch 0 (1970-01-01 00:00:00 UTC).
times_f = (times.astype('datetime64[ns]').astype(np.int64) // 10**9).astype(np.float64) / 60 / 60 / 24 / 365.25
print(f"times_f.shape: {times_f.shape}")
times_ftimes_f.shape: (4632,)
Index([ 40.0, 40.002737850787135, 40.00547570157426,
40.0082135523614, 40.01095140314853, 40.01368925393566,
...
52.67077344284736, 52.6735112936345, 52.67624914442163,
52.67898699520876],
dtype='float64', length=4632)Utility functions
Code to fit a model and plot the results:
import concurrent.futures
def sample(model, draws=500, tune=1000, chains=4, cores=4,
compute_convergence_checks=True,
sample_posterior_predictive=True,
compute_log_likelihood=True,
nuts_sampler='pymc'):
"""
Sample from a PyMC3 model and return the InferenceData and LOO.
Parameters
----------
model: PyMC3 model
draws: int
Number of draws from the posterior distribution
tune: int
Number of tuning steps
chains: int
Number of chains
cores: int
Number of cores
sample_prior_predictive: bool
Weheter to sample prior predictive
compute_convergence_checks: bool
Whether to compute convergence checks
sample_posterior_predictive: bool
Whether to sample posterior predictive
compute_log_likelihood: bool
Whether to compute log likelihood
nuts_sampler: str
NUTS sampler to use. One of 'pymc', 'blackjax', 'numpyro', 'nutpie'
Returns
-------
idata: InferenceData
InferenceData object
"""
assert nuts_sampler in ['pymc', 'blackjax', 'numpyro', 'nutpie']
with model:
print(f"Sampling {draws} draws, {tune} tune, {chains} chains, {cores} cores")
idata = pm.sample(draws=draws, tune=tune, chains=chains, cores=cores,
compute_convergence_checks=compute_convergence_checks,
return_inferencedata=True, nuts_sampler=nuts_sampler,
idata_kwargs={'log_likelihood': False})
if sample_posterior_predictive:
# sample posterior predictive
print(f"Sampling posterior predictive")
pm.sample_posterior_predictive(idata, extend_inferencedata=True, return_inferencedata=True)
if compute_log_likelihood:
# compute log likelihood
print(f"Computing log likelihood")
pm.compute_log_likelihood(idata)
# loo = az.loo(idata)
return idata # , loo
def run_model(fn, *args, **kwargs):
"""
Run a function in a separate process and return the result.
This is useful to avoid memory leaks in PyMC.
"""
with concurrent.futures.ProcessPoolExecutor(max_workers=1) as executor:
future = executor.submit(fn, *args, **kwargs)
return future.result()
def plot_summary(idata, var_names, var_posteriors=[], var_ppcs=[], sample_posterior_predictive=True):
if not sample_posterior_predictive:
var_ppcs = []
print("No posterior predictive samples")
# 1 subplot for the trace - 1 for each var of interest
n_rows = len(var_names) + max(len(var_posteriors), len(var_ppcs))
fig, axs = plt.subplots(n_rows, 2, figsize=(20, 5 * n_rows))
# plot the trace
az.plot_trace(idata, var_names=var_names, kind='rank_vlines', axes=np.array(axs[:len(var_names),:]).reshape(len(var_names), 2))
# increase spacing between plots
# plt.subplots_adjust(hspace=0.8)
# plot the posterior
for i, var_of_interest in enumerate(var_posteriors):
az.plot_posterior(idata, var_names=var_of_interest, ax=axs[len(var_names) + i, 0], kind='kde')
axs[i + 1, 0].set_title(f"{var_of_interest} posterior")
# plot the posterior predictive
for i, var_of_interest in enumerate(var_ppcs):
az.plot_ppc(idata, var_names=var_of_interest, ax=axs[len(var_names) + i, 1], kind='kde')
axs[i + 1, 1].set_title(f"{var_of_interest} posterior predictive")
def keep_vars(idata, threshold=65):
"""
Keep only the vars with total dimension smaller than threshold
"""
vars = []
for k in idata.posterior.data_vars:
# ignore 'chain' and 'draw' dimensions and keep only the ones with a product of the remaining dimensions <= threshold
s = idata.posterior[k].shape
sn = idata.posterior[k].dims
shape = 1
for d in sn:
if d not in ['chain', 'draw']:
shape *= s[sn.index(d)]
if shape <= threshold:
vars.append(k)
return vars
def save_idata(idata, filename):
"""
Save the InferenceData to a file
"""
idata.to_netcdf(filename)
def load_idata(filename):
"""
Load the InferenceData from a file
"""
return az.from_netcdf(filename)
def stratify(df, by, target_samples=10000):
"""
Stratify a dataframe by a column and sample each group to have at most target_samples rows.
"""
def sample_(x, target_samples=10000):
if len(x) <= target_samples:
return x
else:
return x.sample(target_samples)
return df.groupby(by, group_keys=False).apply(sample_, target_samples=target_samples)
def plot_ppc(idata, max_years=5, target_samples=10_000, bw_adjust=.2, hist=False):
"""
Plot the posterior predictive check for the model
We want to compare the density of the posterior predictive with the density of the observed data.
We do this for some slices of our models, namely 'stations' and 'years'.
We plot the posterior predictive as a KDE and the observed data as a histogram.
If they are similar, then the model is not too bad.
Parameters
----------
idata: InferenceData
InferenceData object
max_years: int
Maximum number of years to plot for each station. If there are more years, we select evenly spaced years.
target_samples: int
Maximum number of samples to plot for each station and year
bw_adjust: float
Bandwidth adjustment for the KDE - if hist=True
hist: bool - default False
Whether to plot the histogram of the observed data
"""
# prepare the data
ddf = idata.posterior_predictive.to_dataframe().reset_index()
ddf['station'] = ddf['obs_id'].apply(lambda x: x.split('_')[0])
ddf['year'] = ddf['obs_id'].apply(lambda x: x.split('_')[1]).astype(int)
ddf.drop(columns=['obs_id', 'chain', 'draw'], inplace=True)
# stratify the data by station and year
if target_samples is not None:
ddf = stratify(ddf, by=['station', 'year'], target_samples=target_samples)
n_stations = ddf['station'].nunique()
years = ddf['year'].unique()
if len(years) > max_years:
# select evenly spaced years
years = years[np.linspace(0, len(years) - 1, 5, dtype=int)]
n_years = len(years)
fig, ax = plt.subplots(n_stations, n_years, figsize=(1 * n_years, 1 * n_stations), sharex=True, sharey=True)
palette = sns.color_palette("viridis", ddf['year'].nunique())
palette = {
year: palette[i] for i, year in enumerate(ddf['year'].unique())
}
wx_pd_ = wx_pd.reset_index()
for i, s in enumerate(ddf['station'].unique()):
# filter the dataframe for the station
df = ddf[ddf['station'] == s]
wx_pd_s = wx_pd_[wx_pd_['station'] == s]
for j, y in enumerate(years):
df_y = df[df['year'] == y]
wx_pd_s_y = wx_pd_s[wx_pd_s['year'] == y]
if hist:
if len(df_y) > 0:
# plot the posterior predictive - kde
sns.kdeplot(data=df_y, x='temperature', hue='year', ax=ax[i, j], palette=palette, legend=False, linewidth=0.5, bw_adjust=bw_adjust)
# no x-axis label
ax[i, j].set_xlabel(None)
# no y-axis label
# plot the observed data for the station - kde
if len(wx_pd_s_y) > 0:
# sns.kdeplot(data=wx_pd_s, x='TMAX', ax=ax[i, j], hue='year', palette=palette, linestyle='--', label='observed')
# hist of the observed data for the station
sns.histplot(data=wx_pd_s_y, x='TMAX', ax=ax[i, j], color='black', alpha=0.2, legend=False, stat='density')
# no x-axis label
ax[i, j].set_xlabel(None)
# no y-axis label
ax[i, j].set_ylabel(None)
else:
if len(df_y) > 0:
# qqplot
pp_1 = sm.ProbPlot(wx_pd_s_y['TMAX'], fit=False)
pp_2 = sm.ProbPlot(df_y['temperature'], fit=False)
gofplots.qqplot_2samples(pp_1, pp_2, line='45', ax=ax[i, j], xlabel=None, ylabel=None)
# remove labels
ax[i, j].set_ylabel(None)
ax[i, j].set_xlabel(None)
# title only for the first row
if i == 0:
ax[i, j].set_title(f"{y}")
# set title for the row
station_name = wx_pd_s['name'].iloc[0]
# limit to 13 characters
station_name = station_name[:13]
ax[i, 0].set_ylabel(f"{s}\n{station_name}")
# reduce the size of the label
ax[i, 0].yaxis.label.set_size(8)
# set title
if hist:
fig.suptitle('Posterior Predictive (KDE) and Observations (Histogram)')
else:
fig.suptitle('QQplot of Observed and Posterior Predictive Samples')
plt.tight_layout()
# reduce the space between plots - horizontal and vertical
plt.subplots_adjust(wspace=0.05, hspace=0.05)
def trend_station_marker(us_map, idata_df):
"""
Define folium marker for stations
"""
cmap = plt.get_cmap('RdBu_r')
vmin = idata_df['mean'].min()
vmax = idata_df['mean'].max()
# symetrize the colorbar
vmax = max(abs(vmin), abs(vmax))
vmin = -vmax
norm = colors.Normalize(vmin=vmin, vmax=vmax)
for idx, row in idata_df.iterrows():
latitude = row['latitude']
longitude = row['longitude']
name = row['name']
color = cmap(norm(row['mean']))
color = colors.rgb2hex(color)
tip = f"<u>id: {row['station']}</u><br/><b>{name}</b><br/>" + \
f"mean Tmax trend: {row['mean']*10:.4f} C/decade<br/>" + \
f"<b>95% CI: [{row['q_0.025']*10:.4f}, {row['q_0.975']*10:.4f}] C/decade</b><br/>" + \
f"Data from {row['min_date']} to {row['max_date']}."
folium.CircleMarker(location=[latitude, longitude], radius=9, tooltip=tip, color=color, fillColor=color, fillOpacity=0.8).add_to(us_map)
return us_mapModel_0: With per month offset
Simplest model. We assume the temperature is linearly dependent on the time (year) with a per month offset.
The model is: \[ TMAX_{i,j} \sim \mathcal{N}(\beta + \beta_{month_{j}} + \gamma \times year_{j}, \sigma^2) \]
where:
- \(TMAX_{i,j}\) is the maximum temperature measured at station \(i\) at time \(j\)
- \(year_{j}\) is the time in years since Epoch 0 (1970-01-01 00:00:00 UTC)
- \(month_{j}\) is the month of the time of the measure
- \(\beta\) is the average temperature
- \(\beta_{month_{j}}\) is the offset of the temperature for each month
- \(\gamma\) is the slope of the linear relationship between the temperature and the time. \(\gamma \sim \mathcal{N}(0, 1)\)
- \(\sigma\) is the standard deviation of the noise
wx_pd.head()| state | name | latitude | longitude | elevation | county | TMIN | TMAX | year | month | day_of_year | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| date | station | |||||||||||
| 2010-01-01 | USC00043417 | CA | GILROY | 37.0031 | -121.5608 | 59.1 | 6085 | 7.2 | 16.700001 | 2010 | 1 | 1 |
| USC00045123 | CA | LOS GATOS | 37.2319 | -121.9592 | 111.3 | 6085 | 7.8 | 15.000000 | 2010 | 1 | 1 | |
| USC00045933 | CA | MT HAMILTON | 37.3433 | -121.6347 | 1286.3 | 6085 | 2.8 | 10.000000 | 2010 | 1 | 1 | |
| USC00048273 | CA | SKYLINE RIDGE PRESERVE | 37.3133 | -122.1850 | 691.9 | 6085 | 6.1 | 11.100000 | 2010 | 1 | 1 | |
| USR0000CALT | CA | LOS ALTOS CALIFORNIA | 37.3581 | -122.1472 | 196.6 | 6085 | 9.4 | 16.700001 | 2010 | 1 | 1 |
Let’s build the model:
def build_0(stations, wx_pd, time_idxs, times_f):
coords={
"station":stations,
"month": ["Jan", "Feb", "Mar", "Apr", "May", "Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec"],
"obs_id":[f'{loc}_{time.year}_{time.month}_{time.day}' for time, loc in wx_pd.index.values]
}
with pm.Model(coords=coords) as model:
t_ = pm.ConstantData('t', times_f)
month = pm.ConstantData('month', wx_pd['month'].values, dims=['obs_id'])
temp = pm.ConstantData('temp', wx_pd['TMAX'].values, dims=['obs_id'])
# priors
average_temperature = pm.Normal("average_temperature", 20, 10)
month_offset = pm.ZeroSumNormal("month_offset", sigma=5, dims="month")
trend = pm.Normal("trend", 0, 1)
expected_temperature = pm.Deterministic(
"expected_temperature",
average_temperature +
(trend * t_[time_idxs]) +
month_offset[month - 1],
dims=("obs_id")
)
sigma = pm.HalfNormal("sigma", 5)
# likelihood
pm.Normal("temperature", mu=expected_temperature, sigma=sigma, observed=temp, dims=("obs_id"))
return model
pm.model_to_graphviz(build_0(stations, wx_pd, time_idxs, times_f))
def build_and_sample(stations, wx_pd, time_idxs, times_f,
compute_convergence_checks=True,
sample_posterior_predictive=True,
compute_log_likelihood=True, nuts_sampler='pymc'):
model = build_0(stations, wx_pd, time_idxs, times_f)
idata = sample(model,
compute_convergence_checks=compute_convergence_checks,
sample_posterior_predictive=sample_posterior_predictive,
compute_log_likelihood=compute_log_likelihood,
nuts_sampler=nuts_sampler)
return idata
idata_0 = run_model(build_and_sample, stations, wx_pd, time_idxs, times_f,
compute_convergence_checks=compute_convergence_checks,
sample_posterior_predictive=sample_posterior_predictive,
compute_log_likelihood=compute_log_likelihood,
nuts_sampler=nuts_sampler)
idata_0Sampling 500 draws, 1000 tune, 4 chains, 4 cores
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [average_temperature, month_offset, trend, sigma]100.00% [6000/6000 01:18<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 1_000 tune and 500 draw iterations (4_000 + 2_000 draws total) took 79 seconds.
Sampling posterior predictive
Sampling: [temperature]100.00% [2000/2000 00:01<00:00]
Computing log likelihood100.00% [2000/2000 00:00<00:00]
Posterior predictive checks:
We use a collection of quantile-quantile plots to check if the distribution of the posterior predictive is close to the distribution of the data. Since they are showing quantiles of one vs the quantiles of the other, if the two distributions are the same, the points should be on the diagonal.
plot_ppc(idata_0)
plt.show()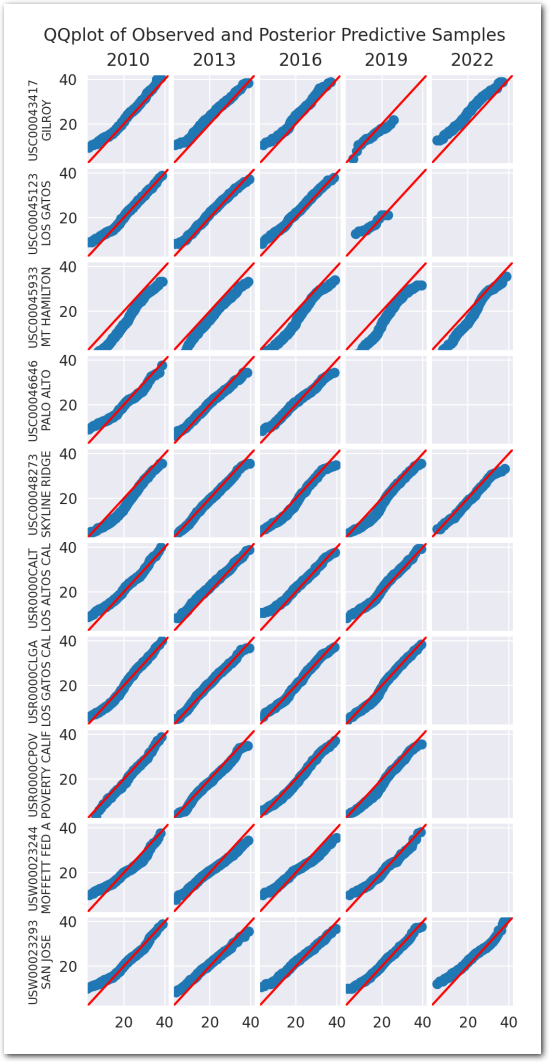
Posteriors for the parameters:
az.summary(idata_0, var_names=['average_temperature', 'trend', 'sigma', 'month_offset'], round_to=3, kind='stats')| mean | sd | hdi_3% | hdi_97% | |
|---|---|---|---|---|
| average_temperature | 17.752 | 0.348 | 17.075 | 18.392 |
| trend | 0.070 | 0.008 | 0.056 | 0.085 |
| sigma | 4.879 | 0.017 | 4.843 | 4.909 |
| month_offset[Jan] | -6.327 | 0.083 | -6.477 | -6.172 |
| month_offset[Feb] | -5.340 | 0.085 | -5.506 | -5.189 |
| month_offset[Mar] | -3.940 | 0.083 | -4.080 | -3.775 |
| month_offset[Apr] | -1.559 | 0.083 | -1.705 | -1.407 |
| month_offset[May] | 0.578 | 0.083 | 0.419 | 0.731 |
| month_offset[Jun] | 5.134 | 0.085 | 4.982 | 5.297 |
| month_offset[Jul] | 6.767 | 0.085 | 6.602 | 6.914 |
| month_offset[Aug] | 6.581 | 0.082 | 6.430 | 6.732 |
| month_offset[Sep] | 6.098 | 0.090 | 5.936 | 6.269 |
| month_offset[Oct] | 2.525 | 0.089 | 2.359 | 2.689 |
| month_offset[Nov] | -3.329 | 0.087 | -3.493 | -3.171 |
| month_offset[Dec] | -7.186 | 0.081 | -7.339 | -7.038 |
plot_summary(idata_0,
var_names=['average_temperature', 'trend', 'sigma', 'month_offset'],
var_posteriors=['trend'],
var_ppcs=['temperature'],
sample_posterior_predictive=sample_posterior_predictive)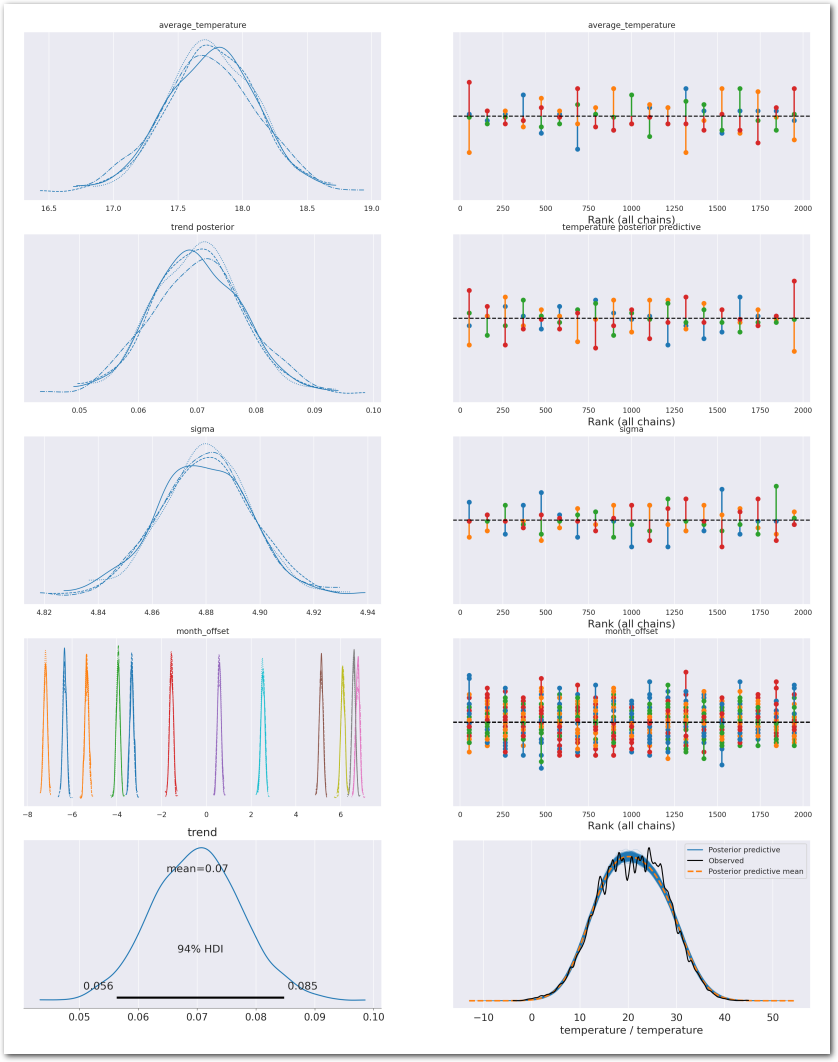
What are the posteriors for the parameters of interest?
az.plot_forest(idata_0, var_names=keep_vars(idata_0),
combined=True, kind='forestplot', hdi_prob=0.95, figsize=(5, 10))
plt.title('Model 0')
plt.show()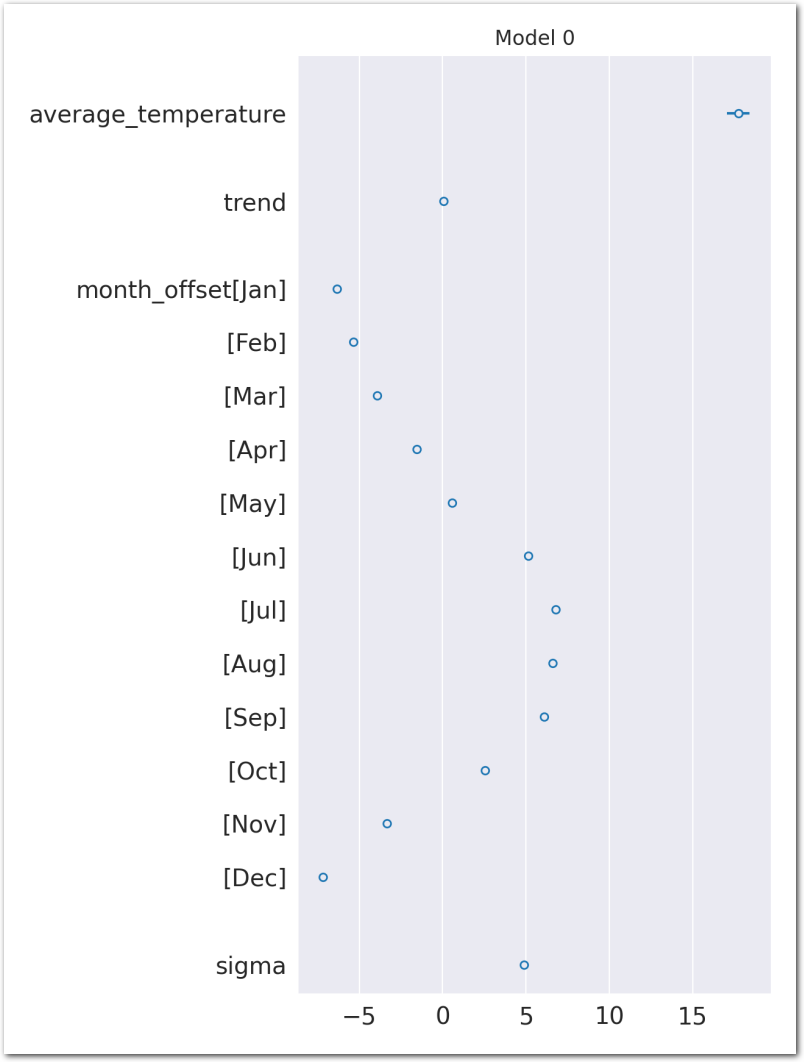
idata_0.posterior['total_trend'] = idata_0.posterior['trend'] Let’s see how the posterior predictive compares to the data on a time series plot for each station:
def plot_posterior_predictive_model(wx_pd, idata, stations_df, station_cmap, sample_posterior_predictive=True):
wx_df_pd = wx_pd[['TMAX']]
new_index = pd.MultiIndex.from_product(wx_df_pd.index.levels)
wx_df_pd = wx_df_pd.reindex(new_index).reset_index()
stations = wx_df_pd['station'].unique()
# grid of plots with a plot for each station
g = sns.FacetGrid(wx_df_pd, row="station", hue="station", aspect=9, height=3, palette=station_cmap, sharex=True)
g.map(pa.lineplot_breaknans, "date", "TMAX", alpha=0.9, linewidth=0.5, zorder=100)
g.set_titles("{row_name}")
g.add_legend()
trend = idata.posterior['total_trend'].mean(dim=['chain', 'draw']).values
trend_ci = az.hdi(idata.posterior['trend'], hdi_prob=0.95)
trend_ci_lower = trend_ci.sel(hdi='lower').trend
trend_ci_higher = trend_ci.sel(hdi='higher').trend
# annotate the trend for each station
for ax, station in zip(g.axes.flat, stations):
ax.annotate(f"trend: {trend*10:.3f}C/decade - 95%CI: [{trend_ci_lower*10:.3f}, {trend_ci_higher*10:.3f}]C/decade",
xy=(0.05, 0.95),
xycoords='axes fraction', fontsize=12,
horizontalalignment='left', verticalalignment='top')
# plot the posterior predictive
if sample_posterior_predictive:
obs_ids = [f'{loc}_{time.year}_{time.month}_{time.day}' for time, loc in wx_pd.index.values if loc == station]
all_times = wx_pd.index.get_level_values(0).unique()
times_station = [time for time, loc in wx_pd.index.values if loc == station]
mean_ppc = idata.posterior_predictive['temperature'].sel(obs_id=obs_ids).mean(dim=['chain', 'draw']).values
# 95%-ci
ci_ppc = az.hdi(idata.posterior_predictive['temperature'].sel(obs_id=obs_ids), hdi_prob=0.95)
lower_ci = ci_ppc.sel(hdi='lower').temperature.values
higher_ci = ci_ppc.sel(hdi='higher').temperature.values
# build dataframe with mean_ppc, lower_ci and higher_ci
station_trend_df = pd.DataFrame({'mean_ppc': mean_ppc, 'lower_ci': lower_ci, 'higher_ci': higher_ci}, index=times_station)
# resample to all_times
station_trend_df = station_trend_df.reindex(all_times)
# plot the mean_ppc
ax.plot(station_trend_df.index, station_trend_df['mean_ppc'], color='red', linewidth=0.5, linestyle='--')
# plot the 95%-CI
ax.fill_between(station_trend_df.index, station_trend_df['lower_ci'], station_trend_df['higher_ci'], color='black', alpha=0.2, linewidth=0.5)
# set the title for each plot with the station id and name
ax.set_title(format_station_name(station, new_line=False))
return g
g = plot_posterior_predictive_model(wx_pd, idata_0, stations_df, station_cmap, sample_posterior_predictive=sample_posterior_predictive)
plt.show()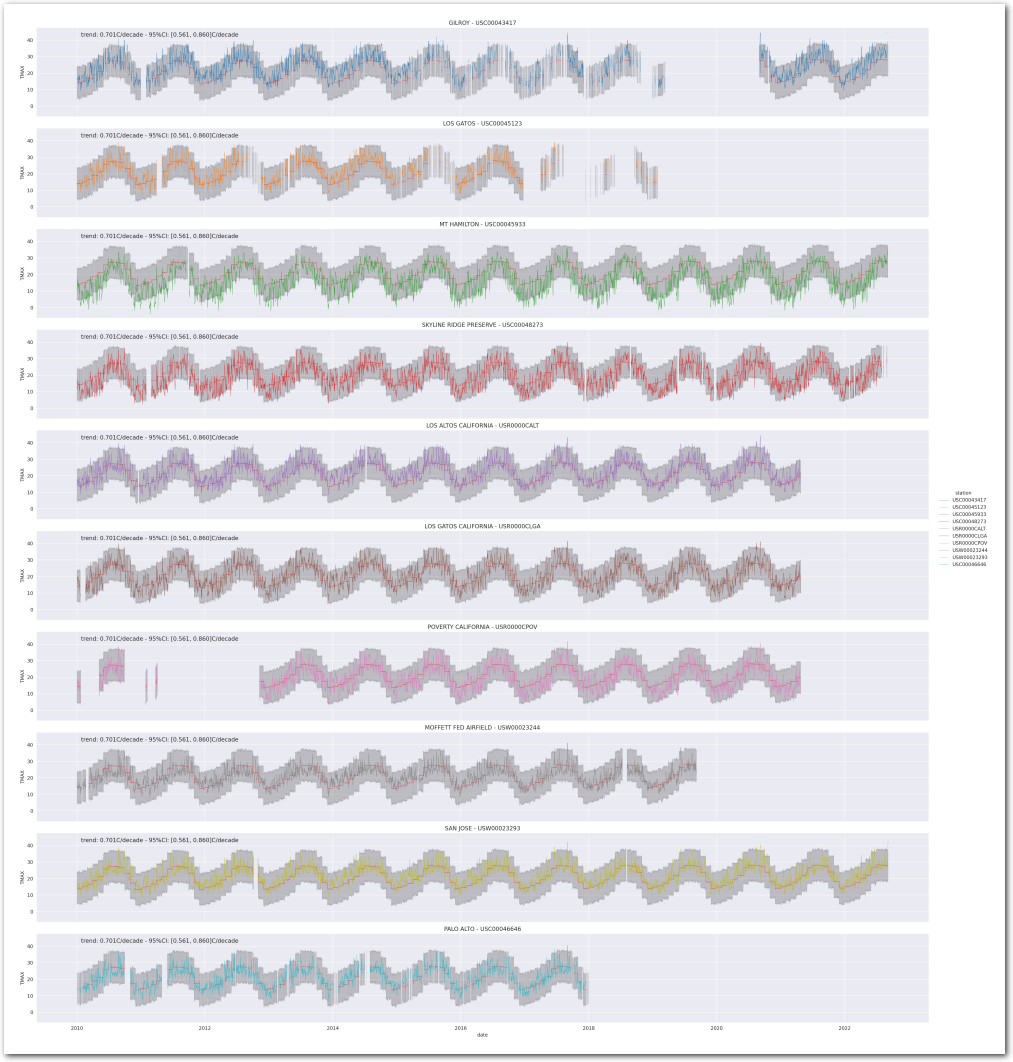
Model_1: With per month offset and per station offset
In this model, we assume the temperature is linearly dependent on the time (year) with a per month offset and a per station offset.
That is: \[ TMAX_{i,j} \sim \mathcal{N}(\beta + \beta_{month_{j}} + \beta_{station_{i}} + \gamma \times year_{j}, \sigma^2) \]
where:
- \(TMAX_{i,j}\) is the maximum temperature measured at station \(i\) at time \(j\)
- \(year_{j}\) is the time in years since Epoch 0 (1970-01-01 00:00:00 UTC)
- \(month_{j}\) is the month of the time of the measure
- \(\beta\) is the average temperature
- \(\beta_{month_{j}}\) is the offset of the temperature for each month with the constraint that \(\sum_{j=1}^{12} \beta_{month_{j}} = 0\)
- \(\beta_{station_{i}}\) is the offset of the temperature for each station with the constraint that \(\sum_{i=1}^{N} \beta_{station_{i}} = 0\)
- \(\gamma\) is the slope of the linear relationship between the temperature and the time. \(\gamma\) is the same for all stations and \(\gamma \sim \mathcal{N}(0, 1)\)
def build_1(stations, wx_pd, time_idxs, times_f, station_idxs):
coords={
"station": stations,
"month": ["Jan", "Feb", "Mar", "Apr", "May", "Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec"],
"obs_id":[f'{loc}_{time.year}_{time.month}_{time.day}' for time, loc in wx_pd.index.values]
}
with pm.Model(coords=coords) as model:
t_ = pm.ConstantData('t', times_f)
month = pm.ConstantData('month', wx_pd['month'].values, dims=['obs_id'])
temp = pm.ConstantData('temp', wx_pd['TMAX'].values, dims=['obs_id'])
# priors
average_temperature = pm.Normal("average_temperature", 20, 10)
month_offset = pm.ZeroSumNormal("month_offset", sigma=5, dims="month")
trend = pm.Normal("trend", 0, 1)
station_offset = pm.ZeroSumNormal("station_offset", sigma=3.0, dims="station")
expected_temperature = pm.Deterministic(
"expected_temperature",
average_temperature +
(trend * t_[time_idxs]) +
month_offset[month - 1] +
station_offset[station_idxs],
dims=("obs_id")
)
sigma = pm.HalfNormal("sigma", 5)
# likelihood
pm.Normal("temperature", mu=expected_temperature, sigma=sigma, observed=temp, dims=("obs_id"))
return model
pm.model_to_graphviz(build_1(stations, wx_pd, time_idxs, times_f, station_idxs))
def build_and_sample(stations, wx_pd, time_idxs, times_f, station_idxs,
compute_convergence_checks=True,
sample_posterior_predictive=True,
compute_log_likelihood=True, nuts_sampler='pymc'):
model = build_1(stations, wx_pd, time_idxs, times_f, station_idxs)
idata = sample(model,
compute_convergence_checks=compute_convergence_checks,
sample_posterior_predictive=sample_posterior_predictive,
compute_log_likelihood=compute_log_likelihood,
nuts_sampler=nuts_sampler)
return idata
idata_1 = run_model(build_and_sample, stations, wx_pd, time_idxs, times_f, station_idxs,
compute_convergence_checks=compute_convergence_checks,
sample_posterior_predictive=sample_posterior_predictive,
compute_log_likelihood=compute_log_likelihood,
nuts_sampler=nuts_sampler)
idata_1Sampling 500 draws, 1000 tune, 4 chains, 4 cores
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [average_temperature, month_offset, trend, station_offset, sigma]100.00% [6000/6000 02:14<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 1_000 tune and 500 draw iterations (4_000 + 2_000 draws total) took 134 seconds.
Sampling posterior predictive
Sampling: [temperature]100.00% [2000/2000 00:01<00:00]
Computing log likelihood100.00% [2000/2000 00:00<00:00]
Posterior predictive checks:
plot_ppc(idata_1)
plt.show()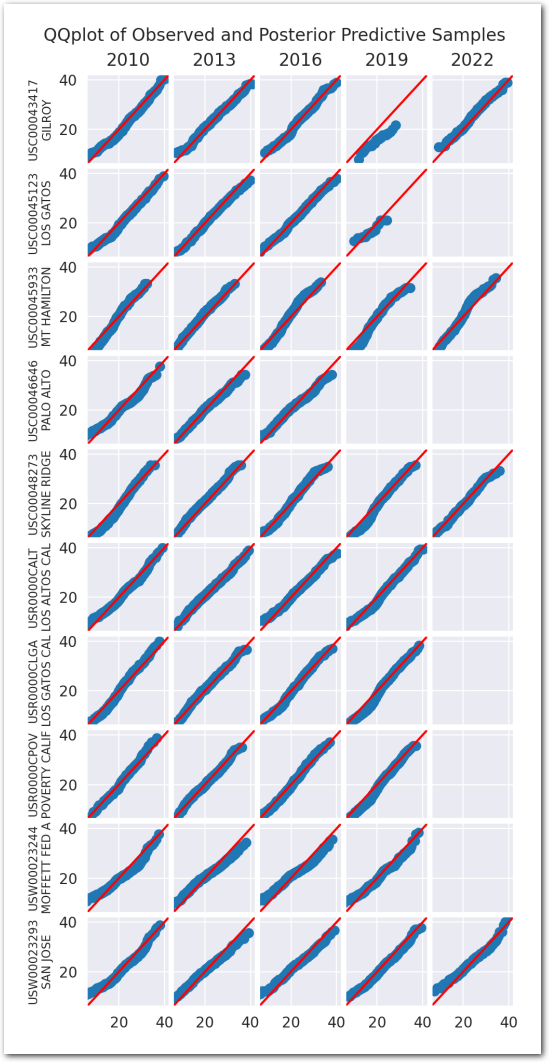
az.summary(idata_1, var_names=['average_temperature', 'trend', 'sigma', 'month_offset', 'station_offset'], round_to=3, kind='stats')| mean | sd | hdi_3% | hdi_97% | |
|---|---|---|---|---|
| average_temperature | 14.730 | 0.320 | 14.185 | 15.376 |
| trend | 0.140 | 0.007 | 0.126 | 0.152 |
| sigma | 4.415 | 0.017 | 4.384 | 4.447 |
| month_offset[Jan] | -6.312 | 0.074 | -6.446 | -6.171 |
| month_offset[Feb] | -5.377 | 0.077 | -5.529 | -5.238 |
| month_offset[Mar] | -3.939 | 0.074 | -4.086 | -3.815 |
| month_offset[Apr] | -1.569 | 0.073 | -1.705 | -1.429 |
| month_offset[May] | 0.614 | 0.075 | 0.473 | 0.751 |
| month_offset[Jun] | 5.158 | 0.071 | 5.025 | 5.288 |
| month_offset[Jul] | 6.805 | 0.075 | 6.674 | 6.940 |
| month_offset[Aug] | 6.595 | 0.075 | 6.459 | 6.732 |
| month_offset[Sep] | 6.088 | 0.078 | 5.928 | 6.219 |
| month_offset[Oct] | 2.501 | 0.077 | 2.351 | 2.630 |
| month_offset[Nov] | -3.364 | 0.077 | -3.505 | -3.209 |
| month_offset[Dec] | -7.200 | 0.075 | -7.340 | -7.055 |
| station_offset[USC00043417] | 2.945 | 0.069 | 2.820 | 3.077 |
| station_offset[USC00045123] | 1.767 | 0.086 | 1.615 | 1.930 |
| station_offset[USC00045933] | -4.418 | 0.064 | -4.535 | -4.298 |
| station_offset[USC00048273] | -1.915 | 0.064 | -2.039 | -1.801 |
| station_offset[USR0000CALT] | 1.584 | 0.064 | 1.462 | 1.703 |
| station_offset[USR0000CLGA] | 0.084 | 0.066 | -0.043 | 0.205 |
| station_offset[USR0000CPOV] | -1.308 | 0.073 | -1.450 | -1.176 |
| station_offset[USW00023244] | 0.066 | 0.070 | -0.057 | 0.203 |
| station_offset[USW00023293] | 0.911 | 0.059 | 0.801 | 1.024 |
| station_offset[USC00046646] | 0.283 | 0.081 | 0.136 | 0.433 |
plot_summary(idata_1,
var_names=['average_temperature', 'trend', 'sigma', 'month_offset', 'station_offset'],
var_posteriors=['trend'],
var_ppcs=['temperature'],
sample_posterior_predictive=sample_posterior_predictive)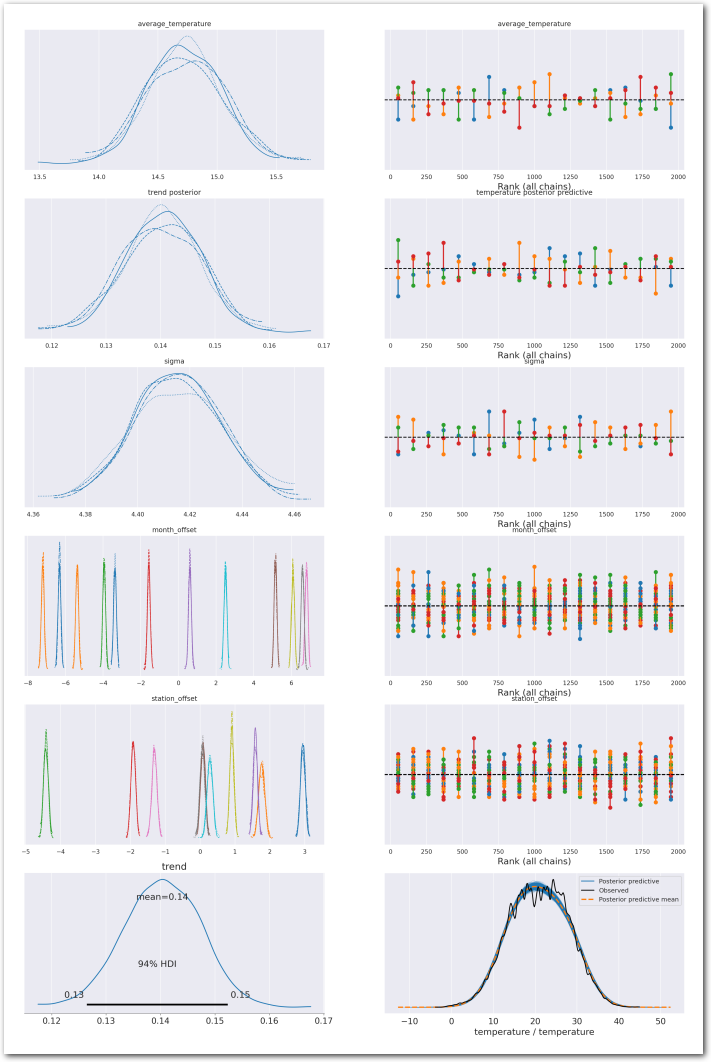
az.plot_forest(idata_1, var_names=keep_vars(idata_1),
combined=True, kind='forestplot', hdi_prob=0.95, figsize=(10, 20))
plt.axvline(x=0, color='red', linestyle='--')
plt.title('Model 1')
plt.show()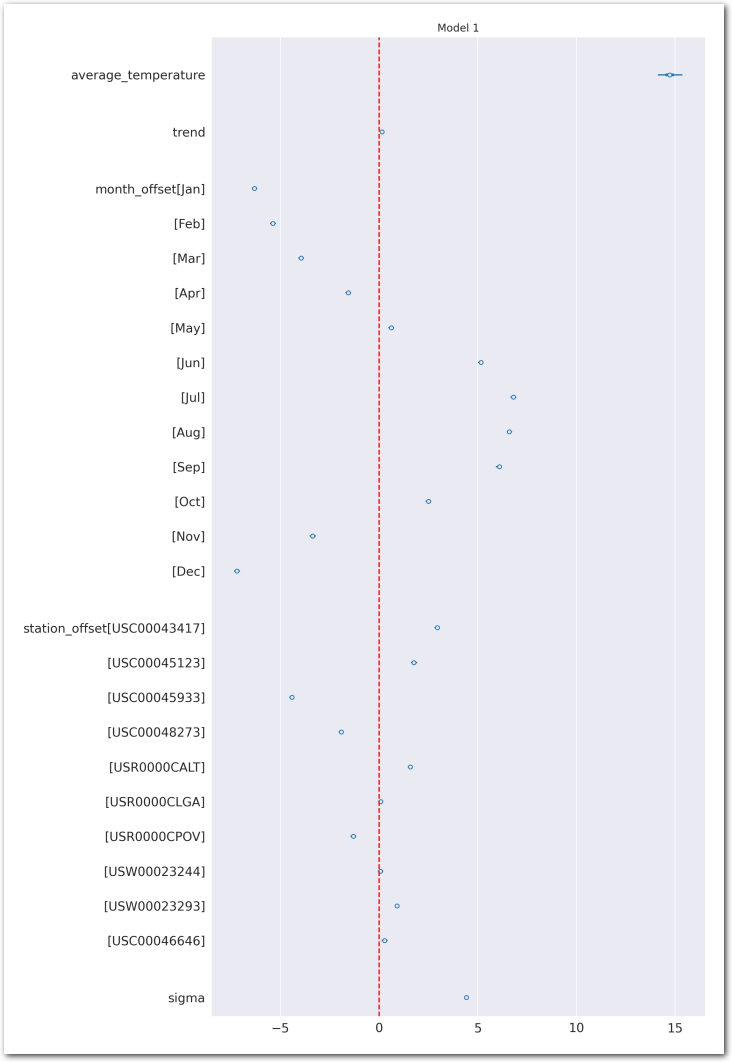
idata_1.posterior['total_trend'] = idata_1.posterior['trend'] Reconstruct the temperature at the stations from the posterior:
g = plot_posterior_predictive_model(wx_pd, idata_1, stations_df, station_cmap, sample_posterior_predictive=sample_posterior_predictive)
plt.show()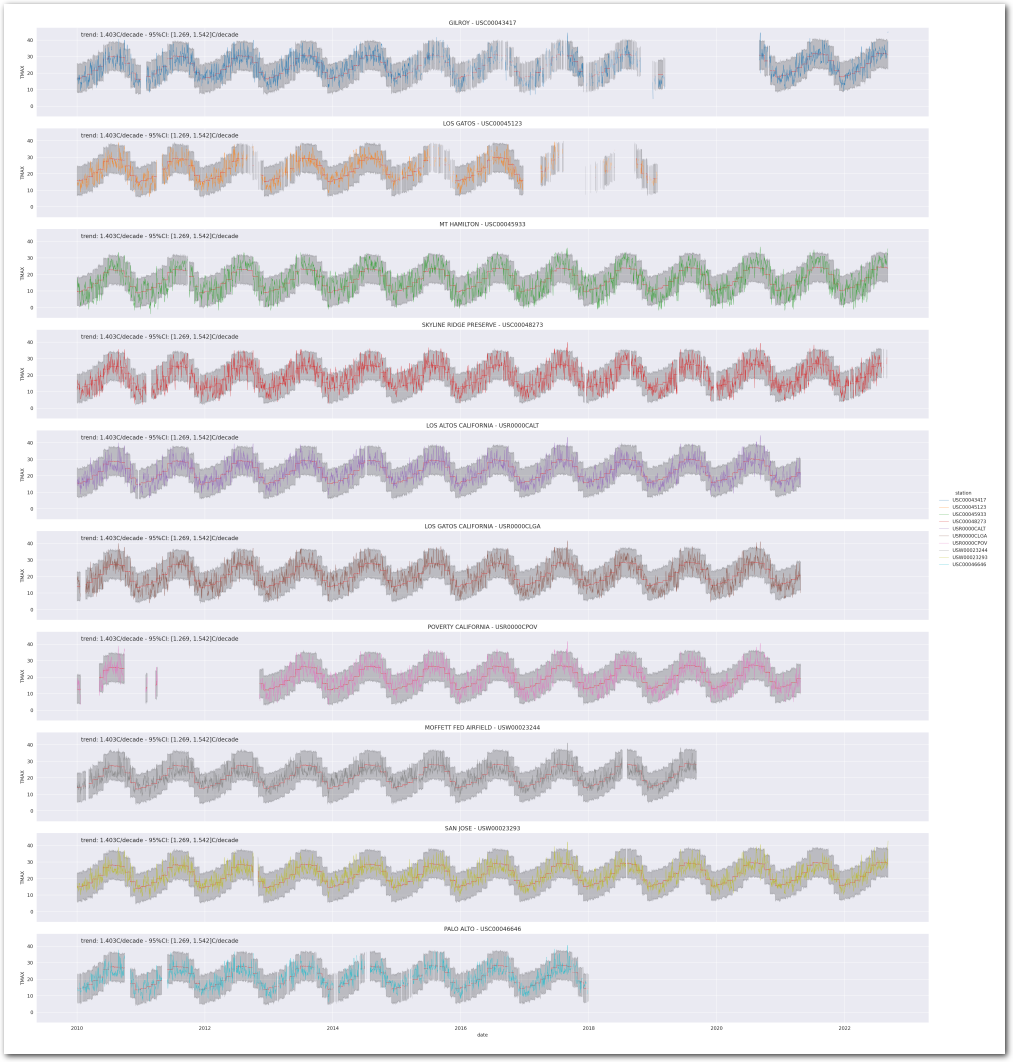
Model_2: With hierarchical trends (per month)
With this model, we assume each month has its own trend that is shared by all stations and we have a per station offset. The temperature is linearly dependent on the time (year) through the trend of the month with a per month offset and a per station offset.
The model is: \[ TMAX_{i,j} \sim \mathcal{N}(\beta + \beta_{month_{j}} + \beta_{station_{i}} + \gamma_{month_{j}} \times year_{j}, \sigma^2) \]
where:
- \(TMAX_{i,j}\) is the maximum temperature measured at station \(i\) at time \(j\)
- \(year_{j}\) is the time in years since Epoch 0 (1970-01-01 00:00:00 UTC)
- \(month_{j}\) is the month of the time of the measure
- \(\beta\) is the average temperature
- \(\beta_{month_{j}}\) is the offset of the temperature for each month with \(\beta_{month_{j}} \sim \mathcal{N}(\mu_{month}, \sigma_{month}^2)\) and the constraint that \(\sum_{j=1}^{12} \beta_{month_{j}} = 0\)
- \(\beta_{station_{i}}\) is the offset of the temperature for each station with \(\beta_{station_{i}} \sim \mathcal{N}(\mu_{station}, \sigma_{station}^2)\) and the constraint that \(\sum_{i=1}^{N} \beta_{station_{i}} = 0\)
- \(\gamma_{month_{j}}\) is the slope of the linear relationship between the temperature and the time for each month with \(\gamma_{month_{j}} \sim \mathcal{N}(\mu^{\gamma}_{month}, (\sigma^{\gamma}_{month})^2)\)
def build_2(stations, wx_pd, time_idxs, times_f, station_idxs):
coords={
"station": stations,
"month": ["Jan", "Feb", "Mar", "Apr", "May", "Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec"],
"obs_id":[f'{loc}_{time.year}_{time.month}_{time.day}' for time, loc in wx_pd.index.values]
}
with pm.Model(coords=coords) as model:
t_ = pm.ConstantData('t', times_f)
month = pm.ConstantData('month', wx_pd['month'].values, dims=['obs_id'])
temp = pm.ConstantData('temp', wx_pd['TMAX'].values, dims=['obs_id'])
# priors
average_temperature = pm.Normal("average_temperature", 20, 10)
month_offset = pm.ZeroSumNormal("month_offset", sigma=5, dims="month")
trend_mu = pm.Normal("trend_mu", 0, 1)
trend_sigma = pm.HalfNormal("trend_sigma", 1)
trend_month = pm.Normal("trend_month", mu=trend_mu, sigma=trend_sigma, dims="month")
station_offset = pm.ZeroSumNormal("station_offset", sigma=3.0, dims="station")
expected_temperature = pm.Deterministic(
"expected_station_temperature",
average_temperature +
(trend_month[month - 1] * t_[time_idxs]) +
month_offset[month - 1] +
station_offset[station_idxs],
dims=("obs_id")
)
sigma = pm.HalfNormal("sigma", 5)
# likelihood
pm.Normal("temperature", mu=expected_temperature, sigma=sigma, observed=temp, dims=("obs_id"))
return model
pm.model_to_graphviz(build_2(stations, wx_pd, time_idxs, times_f, station_idxs))
def build_and_sample(stations, wx_pd, time_idxs, times_f, station_idxs,
compute_convergence_checks=True,
sample_posterior_predictive=True,
compute_log_likelihood=True, nuts_sampler='pymc'):
model = build_2(stations, wx_pd, time_idxs, times_f, station_idxs)
idata = sample(model,
compute_convergence_checks=compute_convergence_checks,
sample_posterior_predictive=sample_posterior_predictive,
compute_log_likelihood=compute_log_likelihood,
nuts_sampler=nuts_sampler)
return idata
idata_2 = run_model(build_and_sample, stations, wx_pd, time_idxs, times_f, station_idxs,
compute_convergence_checks=compute_convergence_checks,
sample_posterior_predictive=sample_posterior_predictive,
compute_log_likelihood=compute_log_likelihood,
nuts_sampler=nuts_sampler)
idata_2Sampling 500 draws, 1000 tune, 4 chains, 4 cores
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [average_temperature, month_offset, trend_mu, trend_sigma, trend_month, station_offset, sigma]100.00% [6000/6000 04:54<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 1_000 tune and 500 draw iterations (4_000 + 2_000 draws total) took 295 seconds.
Sampling posterior predictive
Sampling: [temperature]100.00% [2000/2000 00:01<00:00]
Computing log likelihood100.00% [2000/2000 00:01<00:00]
Posterior predictive checks:
plot_ppc(idata_2)
plt.show()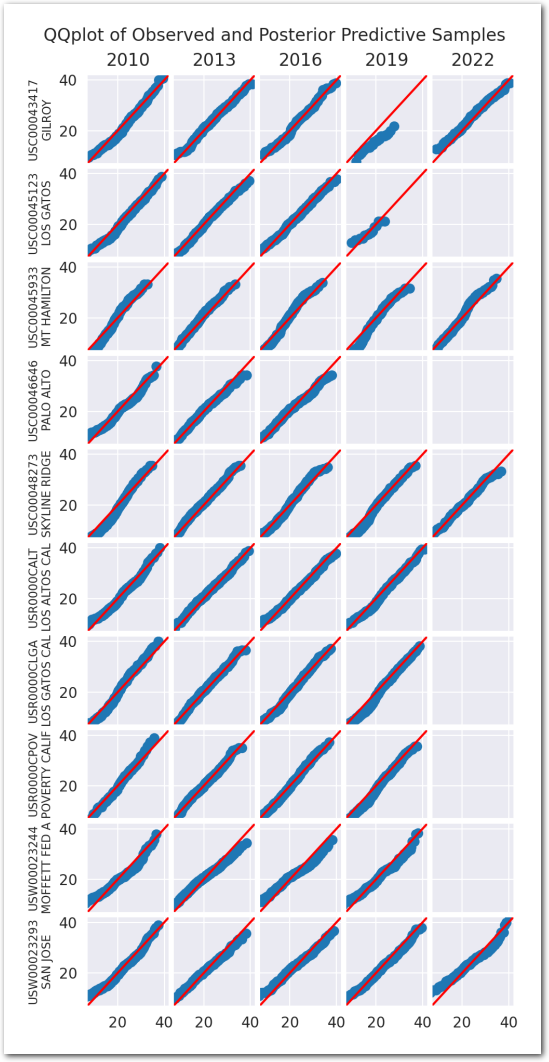
Posteriors:
az.summary(idata_2,
var_names=['average_temperature', 'trend_mu', 'trend_month',
'trend_sigma', 'sigma', 'month_offset', 'station_offset'],
round_to=3, kind='stats')| mean | sd | hdi_3% | hdi_97% | |
|---|---|---|---|---|
| average_temperature | 14.559 | 0.333 | 13.941 | 15.173 |
| trend_mu | 0.143 | 0.038 | 0.071 | 0.215 |
| trend_month[Jan] | 0.006 | 0.021 | -0.034 | 0.047 |
| trend_month[Feb] | 0.084 | 0.023 | 0.041 | 0.125 |
| trend_month[Mar] | -0.047 | 0.021 | -0.083 | -0.007 |
| trend_month[Apr] | 0.115 | 0.023 | 0.072 | 0.156 |
| trend_month[May] | 0.156 | 0.022 | 0.114 | 0.196 |
| trend_month[Jun] | 0.238 | 0.022 | 0.197 | 0.279 |
| trend_month[Jul] | 0.210 | 0.022 | 0.167 | 0.250 |
| trend_month[Aug] | 0.311 | 0.023 | 0.271 | 0.354 |
| trend_month[Sep] | 0.136 | 0.024 | 0.091 | 0.179 |
| trend_month[Oct] | 0.216 | 0.025 | 0.167 | 0.261 |
| trend_month[Nov] | 0.237 | 0.025 | 0.190 | 0.280 |
| trend_month[Dec] | 0.065 | 0.025 | 0.023 | 0.113 |
| trend_sigma | 0.122 | 0.032 | 0.073 | 0.182 |
| sigma | 4.400 | 0.017 | 4.367 | 4.433 |
| month_offset[Jan] | -0.036 | 0.933 | -1.850 | 1.654 |
| month_offset[Feb] | -2.621 | 0.986 | -4.366 | -0.764 |
| month_offset[Mar] | 4.794 | 0.899 | 3.124 | 6.460 |
| month_offset[Apr] | -0.256 | 1.000 | -2.040 | 1.594 |
| month_offset[May] | 0.081 | 0.965 | -1.755 | 1.880 |
| month_offset[Jun] | 0.867 | 0.957 | -1.008 | 2.539 |
| month_offset[Jul] | 3.786 | 0.954 | 1.983 | 5.521 |
| month_offset[Aug] | -1.061 | 0.996 | -2.921 | 0.744 |
| month_offset[Sep] | 6.472 | 1.033 | 4.665 | 8.535 |
| month_offset[Oct] | -0.797 | 1.074 | -2.831 | 1.255 |
| month_offset[Nov] | -7.637 | 1.069 | -9.575 | -5.666 |
| month_offset[Dec] | -3.593 | 1.066 | -5.539 | -1.584 |
| station_offset[USC00043417] | 2.944 | 0.072 | 2.804 | 3.076 |
| station_offset[USC00045123] | 1.762 | 0.082 | 1.607 | 1.909 |
| station_offset[USC00045933] | -4.427 | 0.062 | -4.541 | -4.312 |
| station_offset[USC00048273] | -1.919 | 0.066 | -2.042 | -1.798 |
| station_offset[USR0000CALT] | 1.589 | 0.066 | 1.470 | 1.716 |
| station_offset[USR0000CLGA] | 0.093 | 0.066 | -0.026 | 0.223 |
| station_offset[USR0000CPOV] | -1.291 | 0.074 | -1.430 | -1.153 |
| station_offset[USW00023244] | 0.067 | 0.067 | -0.066 | 0.184 |
| station_offset[USW00023293] | 0.899 | 0.064 | 0.783 | 1.023 |
| station_offset[USC00046646] | 0.283 | 0.085 | 0.125 | 0.444 |
plot_summary(idata_2,
var_names=['average_temperature', 'trend_mu', 'trend_month',
'trend_sigma', 'month_offset', 'station_offset'],
var_posteriors=['trend_mu', 'trend_month'],
var_ppcs=['temperature'],
sample_posterior_predictive=sample_posterior_predictive)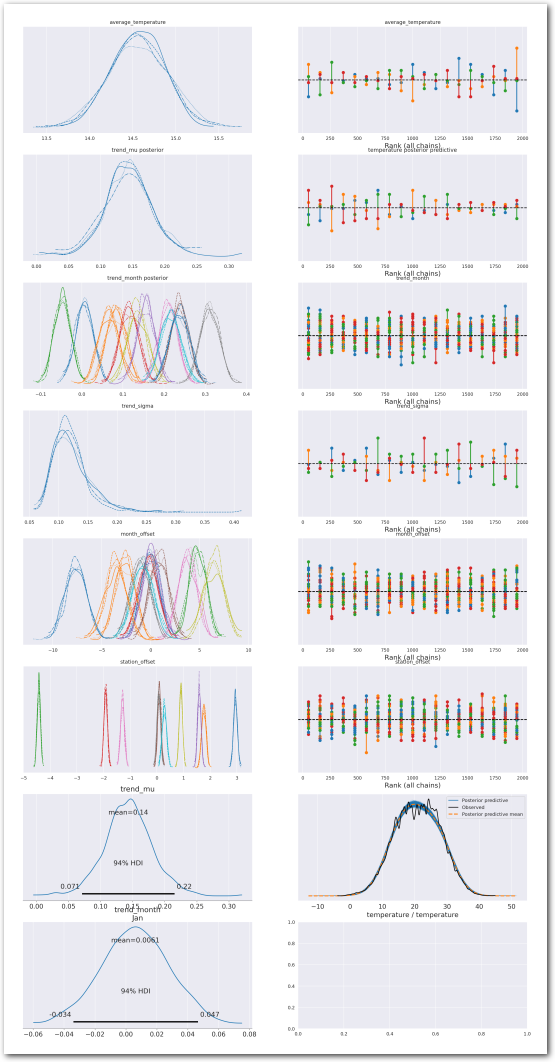
az.plot_forest(idata_2, var_names=keep_vars(idata_2),
combined=True, kind='forestplot', hdi_prob=0.95, figsize=(10, 20))
# vertical dash red line at 0
plt.axvline(x=0, color='red', linestyle='--')
plt.title('Model 2')
plt.show()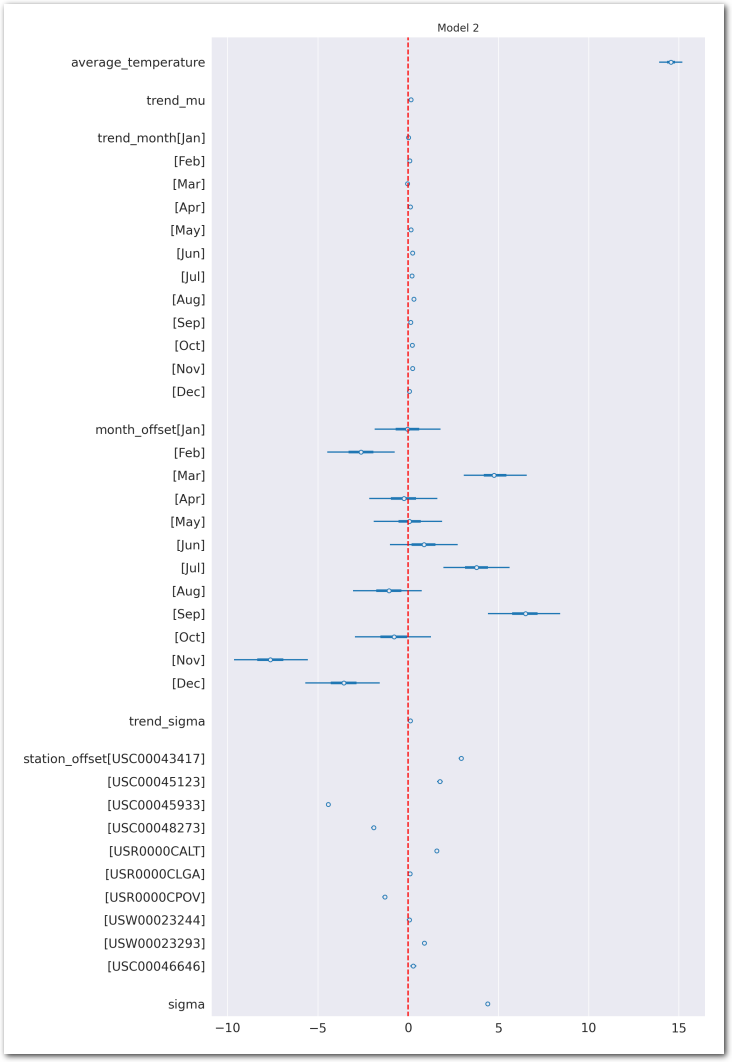
idata_2.posterior['total_trend'] = idata_2.posterior['trend_month'] Reconstruct the temperature at the stations from the posterior:
def plot_posterior_predictive_model_alt(wx_pd, idata, stations_df, station_cmap, sample_posterior_predictive=True, color_trend=True):
wx_df_pd = wx_pd[['TMAX']]
new_index = pd.MultiIndex.from_product(wx_df_pd.index.levels)
wx_df_pd = wx_df_pd.reindex(new_index).reset_index()
stations = wx_df_pd['station'].unique()
# grid of plots with a plot for each station
g = sns.FacetGrid(wx_df_pd, row="station", hue="station", aspect=9, height=3, palette=station_cmap, sharex=True)
g.map(pa.lineplot_breaknans, "date", "TMAX", alpha=0.9, linewidth=0.5, zorder=100)
g.set_titles("{row_name}")
g.add_legend()
cmap = plt.get_cmap('RdBu_r')
trend_min = idata.posterior['total_trend'].min().values
trend_max = idata.posterior['total_trend'].max().values
# symetrize the norm
trend_max = max(abs(trend_min), abs(trend_max))
trend_min = -trend_max
norm = colors.Normalize(vmin=trend_min, vmax=trend_max)
coords = list(idata.posterior['total_trend'].coords)
if 'month' in coords:
trend = idata.posterior['total_trend'].mean(dim=['chain', 'draw']).mean(dim=['month'])
trend_ci_lower = idata.posterior['total_trend'].quantile(0.025, dim=['chain', 'draw']).mean(dim=['month'])
trend_ci_higher = idata.posterior['total_trend'].quantile(0.975, dim=['chain', 'draw']).mean(dim=['month'])
else:
trend = idata.posterior['total_trend'].mean(dim=['chain', 'draw'])
trend_ci_lower = idata.posterior['total_trend'].quantile(0.025, dim=['chain', 'draw'])
trend_ci_higher = idata.posterior['total_trend'].quantile(0.975, dim=['chain', 'draw'])
# annotate the trend for each station
for ax, station in zip(g.axes.flat, stations):
if 'station' in coords:
trend_ = trend.sel(station=station).values
trend_ci_lower_ = trend_ci_lower.sel(station=station).values
trend_ci_higher_ = trend_ci_higher.sel(station=station).values
else:
trend_ = trend.values
trend_ci_lower_ = trend_ci_lower.values
trend_ci_higher_ = trend_ci_higher.values
ax.annotate(f"trend (averaged over months): {trend_*10:.3f}C/decade - 95%CI: [{trend_ci_lower_*10:.3f}, {trend_ci_higher_*10:.3f}]C/decade",
xy=(0.05, 0.95), xycoords='axes fraction', fontsize=12,
horizontalalignment='left', verticalalignment='top')
# plot the posterior predictive
if sample_posterior_predictive:
obs_ids = [f'{loc}_{time.year}_{time.month}_{time.day}' for time, loc in wx_pd.index.values if loc == station]
all_times = wx_pd.index.get_level_values(0).unique()
times_station = [time for time, loc in wx_pd.index.values if loc == station]
mean_ppc = idata.posterior_predictive['temperature'].sel(obs_id=obs_ids).mean(dim=['chain', 'draw']).values
# 95%-ci
ci_ppc = az.hdi(idata.posterior_predictive['temperature'].sel(obs_id=obs_ids), hdi_prob=0.95)
lower_ci = ci_ppc.sel(hdi='lower').temperature.values
higher_ci = ci_ppc.sel(hdi='higher').temperature.values
# build dataframe with mean_ppc, lower_ci and higher_ci
station_trend_df = pd.DataFrame({'mean_ppc': mean_ppc, 'lower_ci': lower_ci, 'higher_ci': higher_ci}, index=times_station)
# resample to all_times
station_trend_df = station_trend_df.reindex(all_times)
# plot the mean_ppc
ax.plot(station_trend_df.index, station_trend_df['mean_ppc'], color='red', linewidth=0.5, linestyle='--')
# plot the 95%-CI
ax.fill_between(station_trend_df.index, station_trend_df['lower_ci'], station_trend_df['higher_ci'], color='black', alpha=0.2, linewidth=0.5)
if color_trend:
# change the background color of each plot with the trend
ax.set_facecolor(cmap(norm(trend_)))
# set the title for each plot with the station id and name
ax.set_title(format_station_name(station, new_line=False))
return g
# don't color the background with the trend since they are the same for all stations with this model.
g = plot_posterior_predictive_model_alt(wx_pd, idata_2, stations_df, station_cmap, sample_posterior_predictive=sample_posterior_predictive, color_trend=False)
plt.show()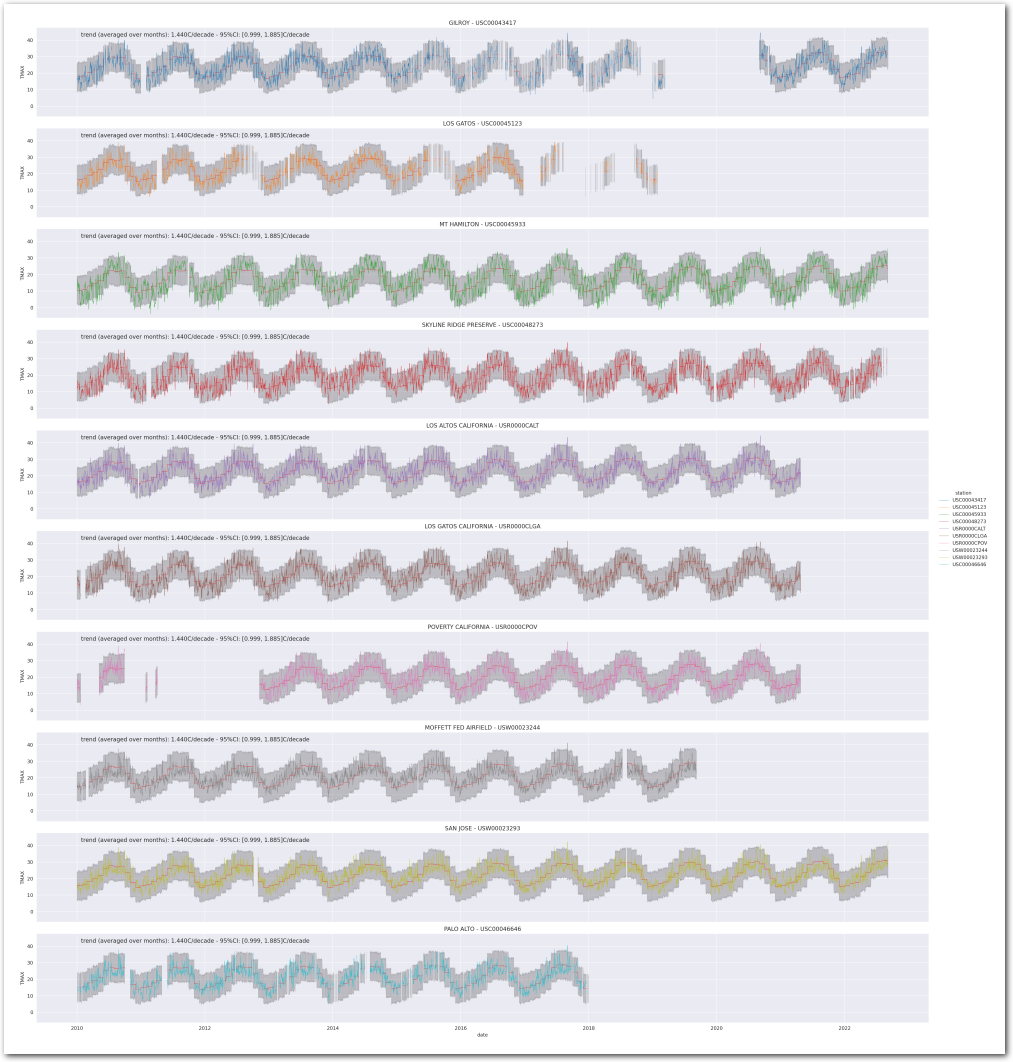
Model_3: With hierarchical trends (per station)
In this model, each station has its own trend that comes from a share distribution of trends and we have a per month offset and per station offset. The temperature is linearly dependent on the time (year) through the trend of the station with a per month offset and a per station offset.
We have: \[ TMAX_{i,j} \sim \mathcal{N}(\beta + \beta_{month_{j}} + \beta_{station_{i}} + \gamma_{station_{i}} \times year_{j}, \sigma^2) \]
where:
- \(TMAX_{i,j}\) is the maximum temperature measured at station \(i\) at time \(j\)
- \(year_{j}\) is the time in years since Epoch 0 (1970-01-01 00:00:00 UTC)
- \(month_{j}\) is the month of the time of the measure
- \(\beta\) is the average temperature
- \(\beta_{month_{j}}\) is the offset of the temperature for each month with the constraint that \(\sum_{j=1}^{12} \beta_{month_{j}} = 0\)
- \(\beta_{station_{i}}\) is the offset of the temperature for each station with \(\beta_{station_{i}} \sim \mathcal{N}(\mu_{station}, \sigma_{station}^2)\) with the additional constraint that \(\sum_{i=1}^{N_{stations}} \beta_{station_{i}} = 0\)
- \(\gamma_{station_{i}}\) is the slope of the linear relationship between the temperature and the time for each station with \(\gamma_{station_{i}} \sim \mathcal{N}(\mu^{\gamma}_{station}, (\sigma^{\gamma}_{station})^2)\)
def build_3(stations, wx_pd, time_idxs, times_f, station_idxs):
coords={
"station": stations,
"month": ["Jan", "Feb", "Mar", "Apr", "May", "Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec"],
"obs_id":[f'{loc}_{time.year}_{time.month}_{time.day}' for time, loc in wx_pd.index.values]
}
with pm.Model(coords=coords) as model:
t_ = pm.ConstantData('t', times_f)
month = pm.ConstantData('month', wx_pd['month'].values, dims=['obs_id'])
temp = pm.ConstantData('temp', wx_pd['TMAX'].values, dims=['obs_id'])
# priors
average_temperature = pm.Normal("average_temperature", 20, 10)
month_offset = pm.ZeroSumNormal("month_offset", sigma=5, dims="month")
trend_mu = pm.Normal("trend_mu", 0, 1)
trend_sigma = pm.HalfNormal("trend_sigma", 1)
trend_station = pm.Normal("trend_station", mu=trend_mu, sigma=trend_sigma, dims="station")
station_offset = pm.ZeroSumNormal("station_offset", sigma=3.0, dims="station")
expected_temperature = pm.Deterministic(
"expected_temperature",
average_temperature +
month_offset[month - 1] +
(trend_station[station_idxs] * t_[time_idxs]) +
station_offset[station_idxs],
dims=("obs_id")
)
sigma = pm.HalfNormal("sigma", 5)
# likelihood
pm.Normal("temperature", mu=expected_temperature, sigma=sigma, observed=temp, dims=("obs_id"))
return model
pm.model_to_graphviz(build_3(stations, wx_pd, time_idxs, times_f, station_idxs))
def build_and_sample(stations, wx_pd, time_idxs, times_f, station_idxs,
compute_convergence_checks=True,
sample_posterior_predictive=True,
compute_log_likelihood=True, nuts_sampler='pymc'):
model = build_3(stations, wx_pd, time_idxs, times_f, station_idxs)
idata = sample(model,
compute_convergence_checks=compute_convergence_checks,
sample_posterior_predictive=sample_posterior_predictive,
compute_log_likelihood=compute_log_likelihood,
nuts_sampler=nuts_sampler)
return idata
idata_3 = run_model(build_and_sample, stations, wx_pd, time_idxs, times_f, station_idxs,
compute_convergence_checks=compute_convergence_checks,
sample_posterior_predictive=sample_posterior_predictive,
compute_log_likelihood=compute_log_likelihood,
nuts_sampler=nuts_sampler)
idata_3Sampling 500 draws, 1000 tune, 4 chains, 4 cores
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [average_temperature, month_offset, trend_mu, trend_sigma, trend_station, station_offset, sigma]100.00% [6000/6000 04:50<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 1_000 tune and 500 draw iterations (4_000 + 2_000 draws total) took 290 seconds.
Sampling posterior predictive
Sampling: [temperature]100.00% [2000/2000 00:01<00:00]
Computing log likelihood100.00% [2000/2000 00:00<00:00]
Posterior predictive checks:
plot_ppc(idata_3)
plt.show()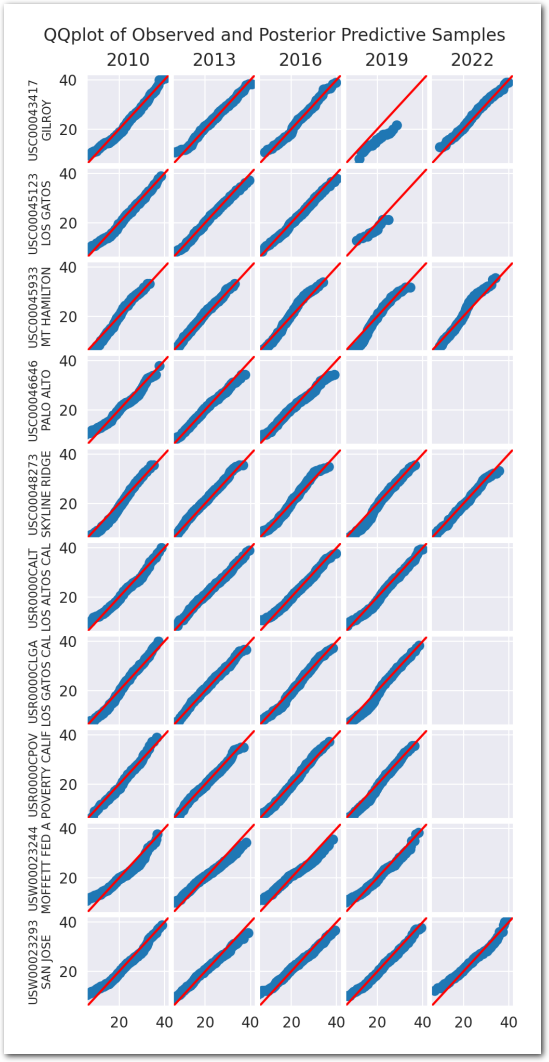
Posteriors:
az.summary(idata_3,
var_names=['average_temperature', 'trend_mu', 'trend_station',
'sigma', 'month_offset', 'station_offset'], round_to=3, kind='stats')| mean | sd | hdi_3% | hdi_97% | |
|---|---|---|---|---|
| average_temperature | 14.264 | 0.365 | 13.638 | 15.017 |
| trend_mu | 0.151 | 0.029 | 0.094 | 0.204 |
| trend_station[USC00043417] | 0.171 | 0.019 | 0.136 | 0.207 |
| trend_station[USC00045123] | 0.292 | 0.036 | 0.228 | 0.357 |
| trend_station[USC00045933] | 0.126 | 0.017 | 0.094 | 0.157 |
| trend_station[USC00048273] | 0.172 | 0.017 | 0.141 | 0.205 |
| trend_station[USR0000CALT] | 0.151 | 0.019 | 0.114 | 0.186 |
| trend_station[USR0000CLGA] | 0.085 | 0.019 | 0.050 | 0.122 |
| trend_station[USR0000CPOV] | 0.060 | 0.024 | 0.016 | 0.105 |
| trend_station[USW00023244] | 0.120 | 0.025 | 0.072 | 0.166 |
| trend_station[USW00023293] | 0.130 | 0.017 | 0.098 | 0.162 |
| trend_station[USC00046646] | 0.208 | 0.031 | 0.149 | 0.266 |
| sigma | 4.412 | 0.017 | 4.381 | 4.445 |
| month_offset[Jan] | -6.309 | 0.071 | -6.434 | -6.173 |
| month_offset[Feb] | -5.365 | 0.077 | -5.526 | -5.229 |
| month_offset[Mar] | -3.927 | 0.076 | -4.061 | -3.779 |
| month_offset[Apr] | -1.576 | 0.073 | -1.709 | -1.436 |
| month_offset[May] | 0.609 | 0.074 | 0.469 | 0.750 |
| month_offset[Jun] | 5.152 | 0.077 | 5.007 | 5.295 |
| month_offset[Jul] | 6.801 | 0.075 | 6.654 | 6.937 |
| month_offset[Aug] | 6.595 | 0.077 | 6.465 | 6.750 |
| month_offset[Sep] | 6.087 | 0.078 | 5.930 | 6.220 |
| month_offset[Oct] | 2.499 | 0.078 | 2.359 | 2.650 |
| month_offset[Nov] | -3.366 | 0.079 | -3.506 | -3.216 |
| month_offset[Dec] | -7.198 | 0.077 | -7.332 | -7.049 |
| station_offset[USC00043417] | 2.018 | 0.847 | 0.479 | 3.600 |
| station_offset[USC00045123] | -4.390 | 1.410 | -7.135 | -1.942 |
| station_offset[USC00045933] | -3.287 | 0.766 | -4.777 | -1.862 |
| station_offset[USC00048273] | -2.923 | 0.753 | -4.298 | -1.447 |
| station_offset[USR0000CALT] | 1.572 | 0.851 | 0.064 | 3.179 |
| station_offset[USR0000CLGA] | 3.071 | 0.854 | 1.456 | 4.633 |
| station_offset[USR0000CPOV] | 2.924 | 1.074 | 1.003 | 5.005 |
| station_offset[USW00023244] | 1.423 | 1.049 | -0.643 | 3.224 |
| station_offset[USW00023293] | 1.836 | 0.772 | 0.326 | 3.297 |
| station_offset[USC00046646] | -2.243 | 1.224 | -4.638 | 0.005 |
plot_summary(idata_3,
var_names=['average_temperature', 'trend_mu', 'trend_station', 'sigma', 'month_offset', 'station_offset'],
var_posteriors=['trend_mu', 'trend_station'],
var_ppcs=['temperature'],
sample_posterior_predictive=sample_posterior_predictive)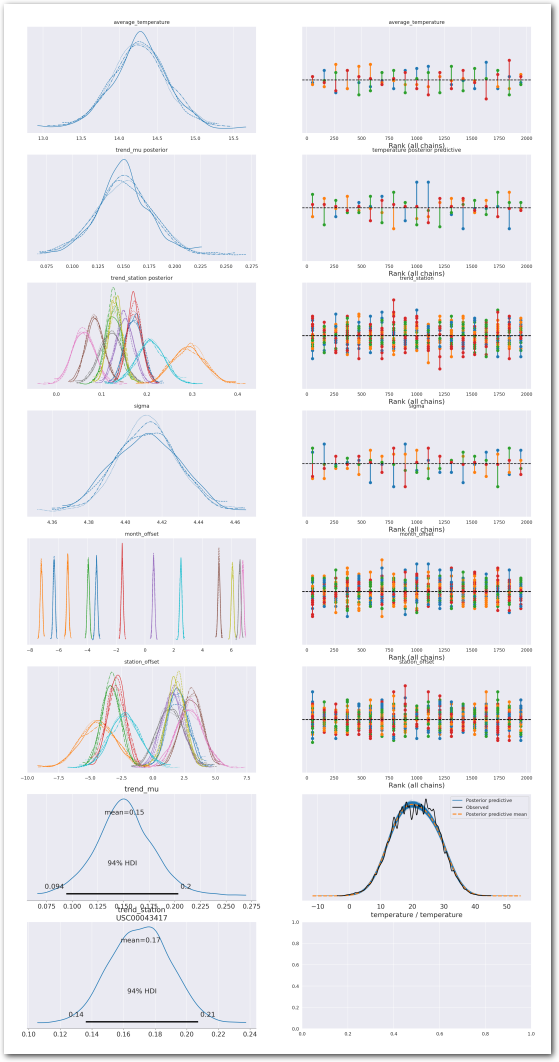
az.plot_forest(idata_3, var_names=keep_vars(idata_3),
combined=True, kind='forestplot', hdi_prob=0.95, figsize=(10, 20))
plt.axvline(x=0, color='red', linestyle='--')
plt.title('Model 3')
plt.show()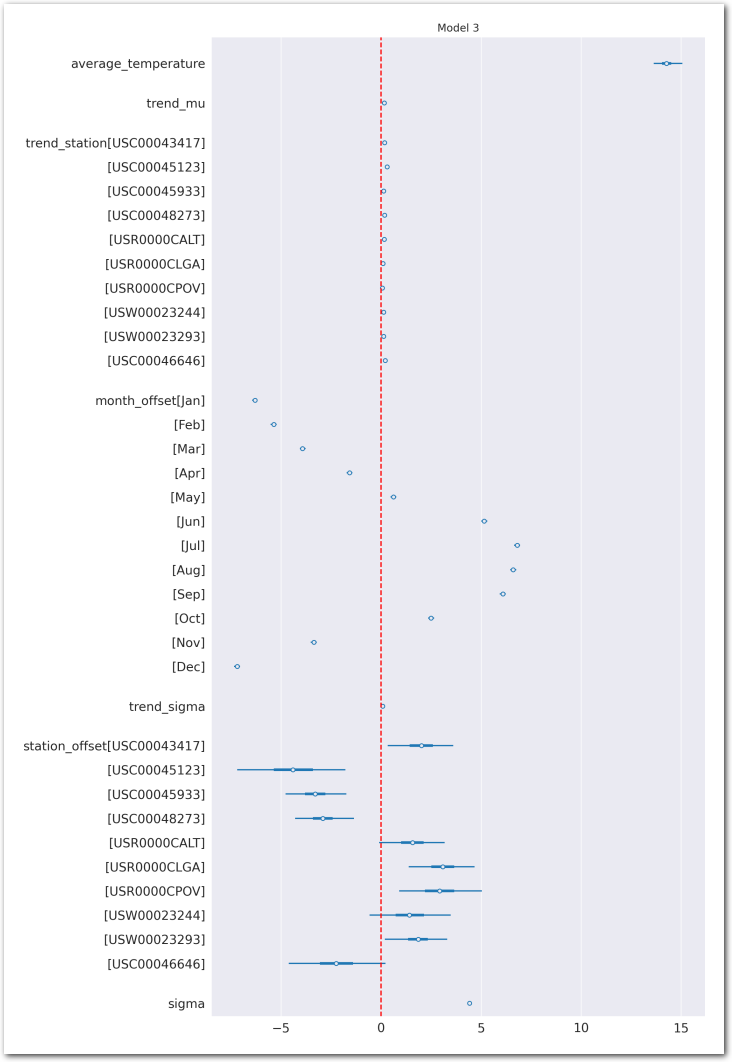
Total trend is:
idata_3.posterior['total_trend'] = idata_3.posterior['trend_station'] Zoom on the trend_station:
def plot_forest_trend_station(idata, counties_stations_heatmap, stations_df, title):
# left subplot with the forest for trend_station, right subplot with the activity heatmap for the stations (same order)
fig, axs = plt.subplots(1, 2, figsize=(20, 10))
az.plot_forest(idata, var_names=['total_trend'], combined=True, kind='forestplot', hdi_prob=0.95, figsize=(20, 10), ax=axs[0])
# red dotted vertical line for the 0 value
axs[0].axvline(0, color='red', linestyle='--')
axs[0].set_title(title)
# plot the heatmap with seaborn
# get the order of the stations in the forest plot - got to extract the station id from the label with a regex (between [ and ])
station_order = [re.search(r'\[(\w+)\]', item.get_text()).group(1) for item in axs[0].get_yticklabels()]
# reversed
station_order = station_order[::-1]
counties_stations_heatmap_ = counties_stations_heatmap.to_pandas()
counties_stations_heatmap_.set_index('date', inplace=True)
# reorder the columns
counties_stations_heatmap_ = counties_stations_heatmap_[station_order]
sns.heatmap(counties_stations_heatmap_.T,
ax=axs[1], cbar=False, cmap='Blues', xticklabels="auto", yticklabels="auto")
axs[1].set_xlabel('Date')
axs[1].set_ylabel('Station')
axs[1].set_title('Stations Activity')
# only show the year on the x-axis
axs[1].set_xticklabels([item.get_text()[:5] for item in axs[1].xaxis.get_ticklabels()])
# set the y-axis labels with the station id and name
axs[1].set_yticklabels([f"{station}\n{stations_df.row(by_predicate=(pl.col('station') == station), named=True)['name']}" for station in station_order])
axs[1].tick_params(axis='y', labelsize=8)
plt.show()
plot_forest_trend_station(idata_3, counties_stations_heatmap, stations_df, title='Model 3')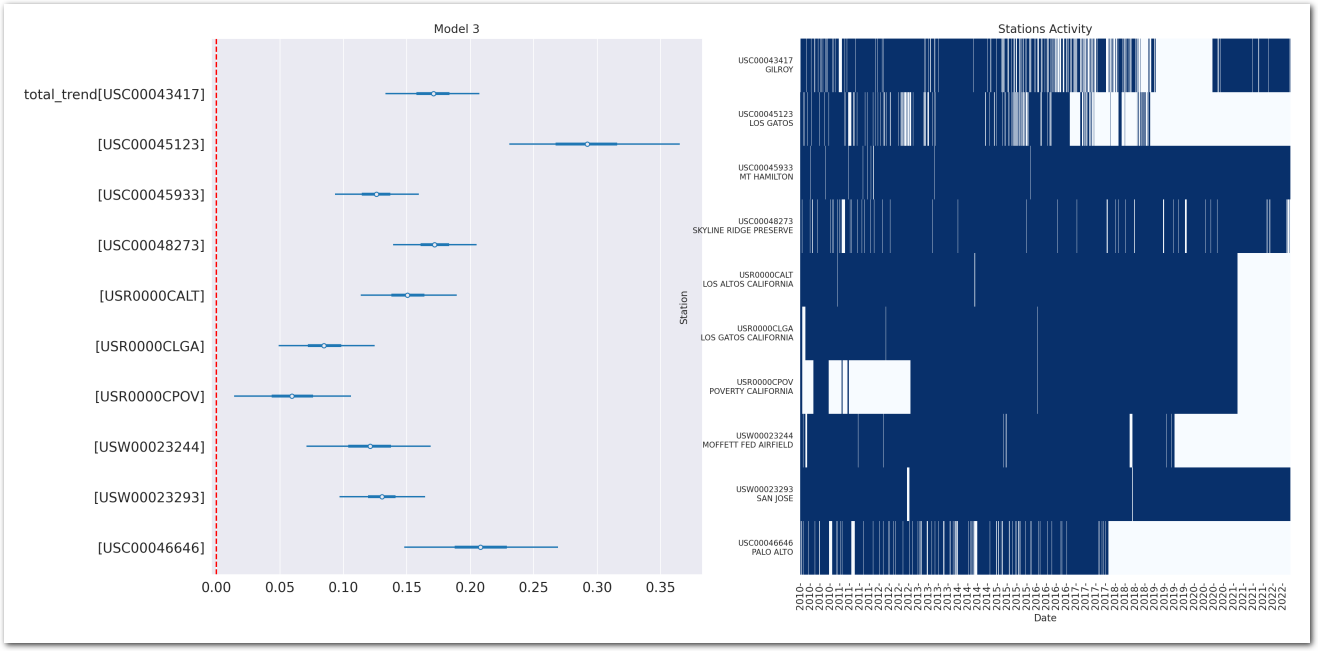
Reconstruct the station temperature from the posterior - the background color is the average trend for each station (blue is negative, red is positive):
g = plot_posterior_predictive_model_alt(wx_pd, idata_3, stations_df, station_cmap, sample_posterior_predictive=sample_posterior_predictive)
plt.show()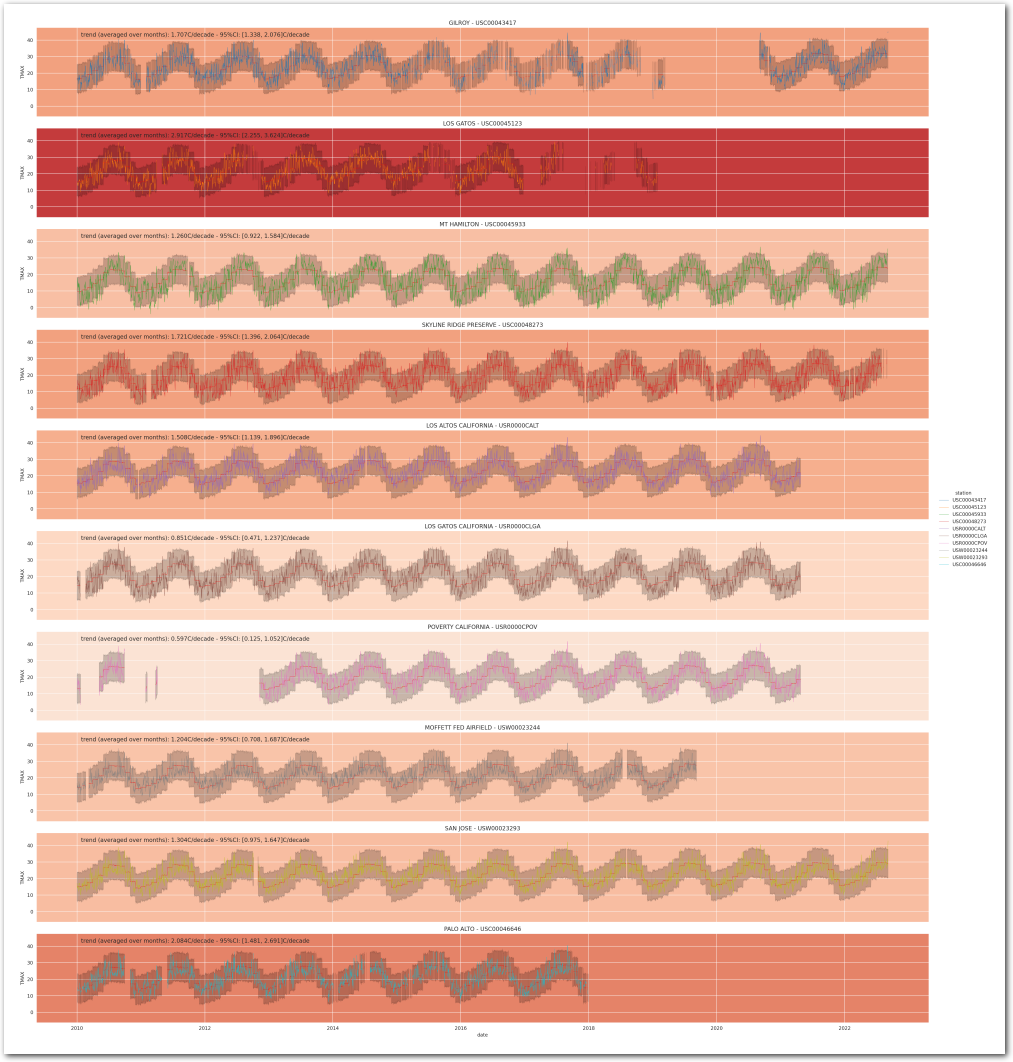
On a map (tooltips on the stations with details):
def summarize_model(idata, counties_stations_df, model_name):
# 95%-ci
idata_df_q = idata.posterior['total_trend'].quantile([0.025, 0.975], dim=['chain', 'draw']).to_dataframe().reset_index().pivot(index='station', columns='quantile', values='total_trend').rename(columns={0.025: 'q_0.025', 0.975: 'q_0.975'})
idata_df_m = idata.posterior['total_trend'].mean(dim=['chain', 'draw']).to_dataframe().reset_index().rename(columns={'total_trend': 'mean'}).set_index('station')
idata_df = pd.concat([idata_df_q, idata_df_m], axis=1)
counties_stations_df_pd = counties_stations_df.to_pandas()
idata_df = idata_df.merge(counties_stations_df_pd[['station', 'latitude', 'longitude', 'name', 'min_date', 'max_date']], left_index=True, right_on='station')
idata_df['month'] = np.nan
idata_df['model'] = model_name
del idata_df_q
del idata_df_m
return idata_df
idata3_df = summarize_model(idata_3, counties_stations_df, model_name='model_3')
idata3_df| q_0.025 | q_0.975 | mean | station | latitude | longitude | name | min_date | max_date | month | model | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 0.133814 | 0.207606 | 0.170737 | USC00043417 | 37.0031 | -121.5608 | GILROY | 2010-01-01 | 2022-09-06 | NaN | model_3 |
| 9 | 0.225476 | 0.362394 | 0.291739 | USC00045123 | 37.2319 | -121.9592 | LOS GATOS | 2010-01-01 | 2019-01-28 | NaN | model_3 |
| 1 | 0.092213 | 0.158439 | 0.126025 | USC00045933 | 37.3433 | -121.6347 | MT HAMILTON | 2010-01-01 | 2022-09-05 | NaN | model_3 |
| 8 | 0.148091 | 0.269118 | 0.208352 | USC00046646 | 37.4436 | -122.1403 | PALO ALTO | 2010-01-02 | 2017-12-30 | NaN | model_3 |
| 2 | 0.139625 | 0.206388 | 0.172080 | USC00048273 | 37.3133 | -122.1850 | SKYLINE RIDGE PRESERVE | 2010-01-01 | 2022-08-31 | NaN | model_3 |
| 3 | 0.113945 | 0.189637 | 0.150795 | USR0000CALT | 37.3581 | -122.1472 | LOS ALTOS CALIFORNIA | 2010-01-01 | 2021-04-25 | NaN | model_3 |
| 4 | 0.047117 | 0.123700 | 0.085117 | USR0000CLGA | 37.2028 | -121.9428 | LOS GATOS CALIFORNIA | 2010-01-01 | 2021-04-25 | NaN | model_3 |
| 7 | 0.012533 | 0.105234 | 0.059700 | USR0000CPOV | 37.4431 | -121.7706 | POVERTY CALIFORNIA | 2010-01-01 | 2021-04-25 | NaN | model_3 |
| 5 | 0.070829 | 0.168674 | 0.120428 | USW00023244 | 37.4058 | -122.0481 | MOFFETT FED AIRFIELD | 2010-01-01 | 2019-09-08 | NaN | model_3 |
| 0 | 0.097460 | 0.164735 | 0.130426 | USW00023293 | 37.3594 | -121.9244 | SAN JOSE | 2010-01-01 | 2022-09-06 | NaN | model_3 |
# plot map with the mean trend_station
us_map = pa.plot_county_geojson(geojson, counties,
zoom_start=8,
markers_fn=lambda m: trend_station_marker(m, idata_df=idata3_df))
us_mapModel_4: With common, per month and per station trends and per station as well as per month and per station offsets
In this model, the total trend is the sum of a common ‘trend’ and ‘trend_offset’ which is both per month and per station.
The temperature is linearly dependent on the time (year) through the total trend of the station with a per month offset and a per station offset.
We have: \[ TMAX_{i,j} \sim \mathcal{N}(\beta + \beta_{month_{j}} + \beta_{station_{i}} + (\gamma + \gamma_{station_{i}} + \gamma_{month_{j}}) \times year_{j}, \sigma^2) \]
where:
- \(TMAX_{i,j}\) is the maximum temperature measured at station \(i\) at time \(j\)
- \(year_{j}\) is the time in years since Epoch 0 (1970-01-01 00:00:00 UTC)
- \(month_{j}\) is the month of the time of the measure
- \(\beta\) is the average temperature
- \(\beta_{month_{j}}\) is the offset of the temperature for each month with \(\beta_{month_{j}} \sim \mathcal{N}(\mu_{month}, \sigma_{month}^2)\) and the constraint that \(\sum_{j=1}^{12} \beta_{month_{j}} = 0\)
- \(\beta_{station_{i}}\) is the offset of the temperature for each station with \(\beta_{station_{i}} \sim \mathcal{N}(\mu_{station}, \sigma_{station}^2)\) and the constraint that \(\sum_{i=1}^{N} \beta_{station_{i}} = 0\)
- \(\gamma\) is the common slope of the linear relationship between the temperature and the time
- \(\gamma_{station_{i}}\) and \(\gamma_{month_{j}}\) are centered Normal distribution.
def build_4(stations, wx_pd, time_idxs, times_f, station_idxs):
coords={
"station": stations,
"month": ["Jan", "Feb", "Mar", "Apr", "May", "Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec"],
"obs_id":[f'{loc}_{time.year}_{time.month}_{time.day}' for time, loc in wx_pd.index.values]
}
with pm.Model(coords=coords) as model:
t_ = pm.ConstantData('t', times_f)
month = pm.ConstantData('month', wx_pd['month'].values, dims=['obs_id'])
temp = pm.ConstantData('temp', wx_pd['TMAX'].values, dims=['obs_id'])
# priors
average_temperature = pm.Normal("average_temperature", 20, 10)
month_offset = pm.ZeroSumNormal("month_offset", sigma=5, dims="month")
trend = pm.Normal("trend", 0, 1)
trend_offset_station_sigma = pm.HalfNormal("trend_offset_station_sigma", 1)
trend_offset_month_sigma = pm.HalfNormal("trend_offset_month_sigma", 1)
trend_offset_station = pm.Normal("trend_offset_station", mu=0, sigma=trend_offset_station_sigma, dims=["station"])
trend_offset_month = pm.Normal("trend_offset_month", mu=0, sigma=trend_offset_month_sigma, dims=["month"])
station_offset = pm.ZeroSumNormal("station_offset", sigma=3.0, dims="station")
expected_temperature = pm.Deterministic(
"expected_temperature",
average_temperature +
month_offset[month - 1] +
((trend + trend_offset_station[station_idxs] + trend_offset_month[month - 1]) * t_[time_idxs]) +
station_offset[station_idxs],
dims=("obs_id")
)
sigma = pm.HalfNormal("sigma", 5)
# likelihood
pm.Normal("temperature", mu=expected_temperature, sigma=sigma, observed=temp, dims=("obs_id"))
return model
pm.model_to_graphviz(build_4(stations, wx_pd, time_idxs, times_f, station_idxs))
def build_and_sample(stations, wx_pd, time_idxs, times_f, station_idxs,
compute_convergence_checks=True,
sample_posterior_predictive=True,
compute_log_likelihood=True, nuts_sampler='pymc'):
model = build_4(stations, wx_pd, time_idxs, times_f, station_idxs)
idata = sample(model,
compute_convergence_checks=compute_convergence_checks,
sample_posterior_predictive=sample_posterior_predictive,
compute_log_likelihood=compute_log_likelihood,
nuts_sampler=nuts_sampler)
return idata
idata_4 = run_model(build_and_sample, stations, wx_pd, time_idxs, times_f, station_idxs,
compute_convergence_checks=compute_convergence_checks,
sample_posterior_predictive=sample_posterior_predictive,
compute_log_likelihood=compute_log_likelihood,
nuts_sampler=nuts_sampler)
idata_4Sampling 500 draws, 1000 tune, 4 chains, 4 cores
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [average_temperature, month_offset, trend, trend_offset_station_sigma, trend_offset_month_sigma, trend_offset_station, trend_offset_month, station_offset, sigma]100.00% [6000/6000 18:38<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 1_000 tune and 500 draw iterations (4_000 + 2_000 draws total) took 1119 seconds.
The effective sample size per chain is smaller than 100 for some parameters. A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
Sampling posterior predictive
Sampling: [temperature]100.00% [2000/2000 00:01<00:00]
Computing log likelihood100.00% [2000/2000 00:01<00:00]
Posterior predictive checks:
plot_ppc(idata_4)
plt.show()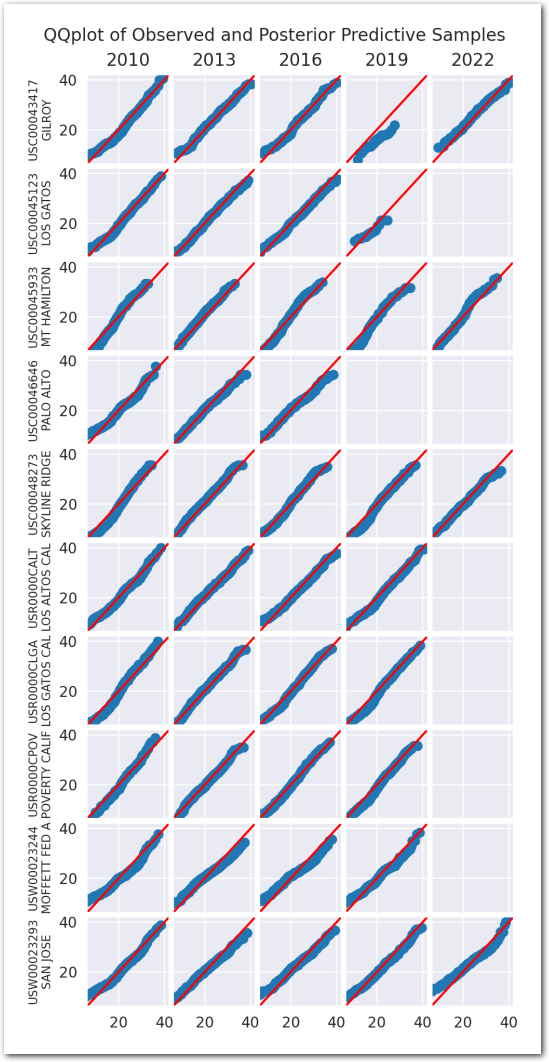
Posteriors:
az.summary(idata_4,
var_names=['average_temperature', 'trend', 'trend_offset_station', 'trend_offset_month', 'sigma', 'month_offset', 'station_offset'],
round_to=3, kind='stats')| mean | sd | hdi_3% | hdi_97% | |
|---|---|---|---|---|
| average_temperature | 14.070 | 0.368 | 13.417 | 14.810 |
| trend | 0.155 | 0.045 | 0.076 | 0.244 |
| trend_offset_station[USC00043417] | 0.018 | 0.031 | -0.043 | 0.072 |
| trend_offset_station[USC00045123] | 0.145 | 0.039 | 0.071 | 0.217 |
| trend_offset_station[USC00045933] | -0.028 | 0.029 | -0.081 | 0.024 |
| trend_offset_station[USC00048273] | 0.021 | 0.030 | -0.034 | 0.076 |
| trend_offset_station[USR0000CALT] | 0.004 | 0.030 | -0.051 | 0.064 |
| trend_offset_station[USR0000CLGA] | -0.062 | 0.031 | -0.124 | -0.007 |
| trend_offset_station[USR0000CPOV] | -0.092 | 0.034 | -0.156 | -0.029 |
| trend_offset_station[USW00023244] | -0.032 | 0.033 | -0.091 | 0.032 |
| trend_offset_station[USW00023293] | -0.023 | 0.030 | -0.078 | 0.034 |
| trend_offset_station[USC00046646] | 0.058 | 0.038 | -0.010 | 0.130 |
| trend_offset_month[Jan] | -0.138 | 0.043 | -0.222 | -0.061 |
| trend_offset_month[Feb] | -0.061 | 0.043 | -0.139 | 0.020 |
| trend_offset_month[Mar] | -0.192 | 0.042 | -0.270 | -0.119 |
| trend_offset_month[Apr] | -0.029 | 0.043 | -0.106 | 0.053 |
| trend_offset_month[May] | 0.011 | 0.042 | -0.070 | 0.086 |
| trend_offset_month[Jun] | 0.095 | 0.043 | 0.008 | 0.169 |
| trend_offset_month[Jul] | 0.067 | 0.043 | -0.007 | 0.152 |
| trend_offset_month[Aug] | 0.168 | 0.042 | 0.091 | 0.247 |
| trend_offset_month[Sep] | -0.009 | 0.043 | -0.089 | 0.070 |
| trend_offset_month[Oct] | 0.071 | 0.044 | -0.011 | 0.151 |
| trend_offset_month[Nov] | 0.092 | 0.042 | 0.008 | 0.166 |
| trend_offset_month[Dec] | -0.078 | 0.043 | -0.160 | -0.001 |
| sigma | 4.397 | 0.016 | 4.368 | 4.426 |
| month_offset[Jan] | -0.029 | 0.957 | -1.788 | 1.751 |
| month_offset[Feb] | -2.584 | 0.986 | -4.451 | -0.787 |
| month_offset[Mar] | 4.809 | 0.959 | 2.991 | 6.538 |
| month_offset[Apr] | -0.269 | 0.951 | -1.893 | 1.688 |
| month_offset[May] | 0.111 | 0.956 | -1.708 | 1.878 |
| month_offset[Jun] | 0.796 | 1.024 | -1.201 | 2.568 |
| month_offset[Jul] | 3.748 | 0.988 | 1.877 | 5.556 |
| month_offset[Aug] | -1.102 | 0.996 | -2.968 | 0.677 |
| month_offset[Sep] | 6.489 | 1.021 | 4.412 | 8.243 |
| month_offset[Oct] | -0.746 | 1.066 | -2.931 | 1.144 |
| month_offset[Nov] | -7.597 | 0.990 | -9.403 | -5.599 |
| month_offset[Dec] | -3.626 | 1.024 | -5.506 | -1.706 |
| station_offset[USC00043417] | 2.103 | 0.824 | 0.469 | 3.558 |
| station_offset[USC00045123] | -4.561 | 1.332 | -7.105 | -1.964 |
| station_offset[USC00045933] | -3.169 | 0.735 | -4.492 | -1.814 |
| station_offset[USC00048273] | -2.897 | 0.781 | -4.287 | -1.386 |
| station_offset[USR0000CALT] | 1.406 | 0.826 | -0.254 | 2.828 |
| station_offset[USR0000CLGA] | 2.935 | 0.866 | 1.392 | 4.681 |
| station_offset[USR0000CPOV] | 2.978 | 1.121 | 0.796 | 4.948 |
| station_offset[USW00023244] | 1.509 | 0.988 | -0.400 | 3.251 |
| station_offset[USW00023293] | 1.964 | 0.767 | 0.519 | 3.409 |
| station_offset[USC00046646] | -2.268 | 1.237 | -4.505 | 0.026 |
plot_summary(idata_4,
var_names=['average_temperature', 'trend', 'trend_offset_station', 'trend_offset_month', 'sigma', 'month_offset', 'station_offset'],
var_posteriors=['trend', 'trend_offset_station', 'trend_offset_month'],
var_ppcs=['temperature'],
sample_posterior_predictive=sample_posterior_predictive)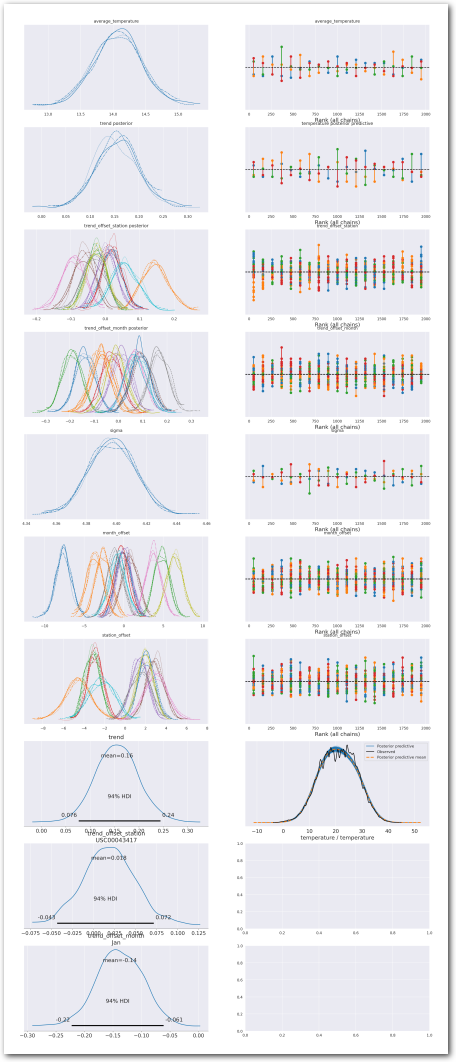
az.plot_forest(idata_4, var_names=keep_vars(idata_4),
combined=True, kind='forestplot', hdi_prob=0.95, figsize=(5, 15))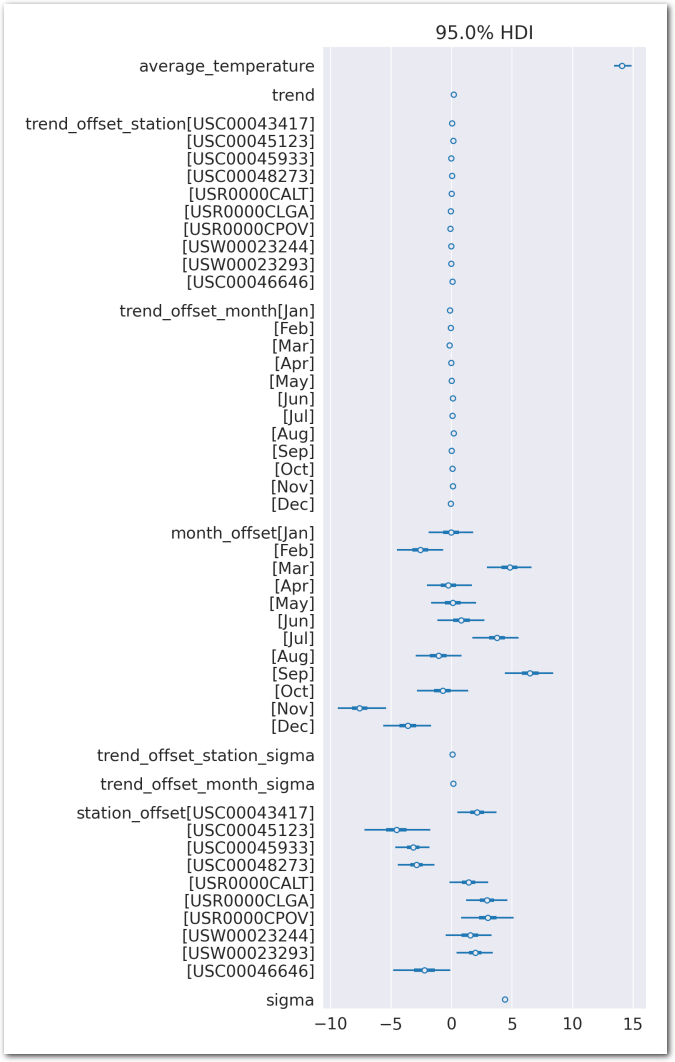
Reconstruct the total trend:
idata_4.posterior['total_trend'] = idata_4.posterior['trend'] + idata_4.posterior['trend_offset_month'] + idata_4.posterior['trend_offset_station']def plot_forest_trend_station_month(idata, counties_stations_heatmap, stations_df, title):
# left subplot with the forest for trend_station, right subplot with the activity heatmap for the stations (same order)
fig, axs = plt.subplots(1, 2, figsize=(16, 15))
# compute the CI for the sum of the trend and trend_offset
months = ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec']
idata_s = [idata.posterior['total_trend'].sel(month=m) for m in months]
az.plot_forest(idata_s, var_names=['total_trend'],
model_names=months,
combined=True, kind='forestplot', hdi_prob=0.95, figsize=(8, 15), ax=axs[0])
axs[0].axvline(0, color='red', linestyle='--')
axs[0].set_title(title)
# plot the heatmap with seaborn
# get the order of the stations in the forest plot - got to extract the station id from the label with a regex (between [ and ])
station_order = [re.search(r'\[(\w+)\]', item.get_text()).group(1) for item in axs[0].get_yticklabels()]
# reversed
station_order = station_order[::-1]
counties_stations_heatmap_ = counties_stations_heatmap.to_pandas()
counties_stations_heatmap_.set_index('date', inplace=True)
# reorder the columns
counties_stations_heatmap_ = counties_stations_heatmap_[station_order]
sns.heatmap(counties_stations_heatmap_.T,
ax=axs[1], cbar=False, cmap='Blues', xticklabels="auto", yticklabels="auto")
axs[1].set_xlabel('Date')
axs[1].set_ylabel('Station')
axs[1].set_title('Stations Activity')
# only show the year on the x-axis
axs[1].set_xticklabels([item.get_text()[:5] for item in axs[1].xaxis.get_ticklabels()])
# add station name to the y-axis
axs[1].set_yticklabels([f"{x}\n{stations_df.row(by_predicate=(pl.col('station') == x), named=True)['name'][:13]}" for x in station_order])
# reduce the font size
axs[1].tick_params(axis='y', which='major', labelsize=6)
plot_forest_trend_station_month(idata_4, counties_stations_heatmap, stations_df, title="Model 4")
plt.show()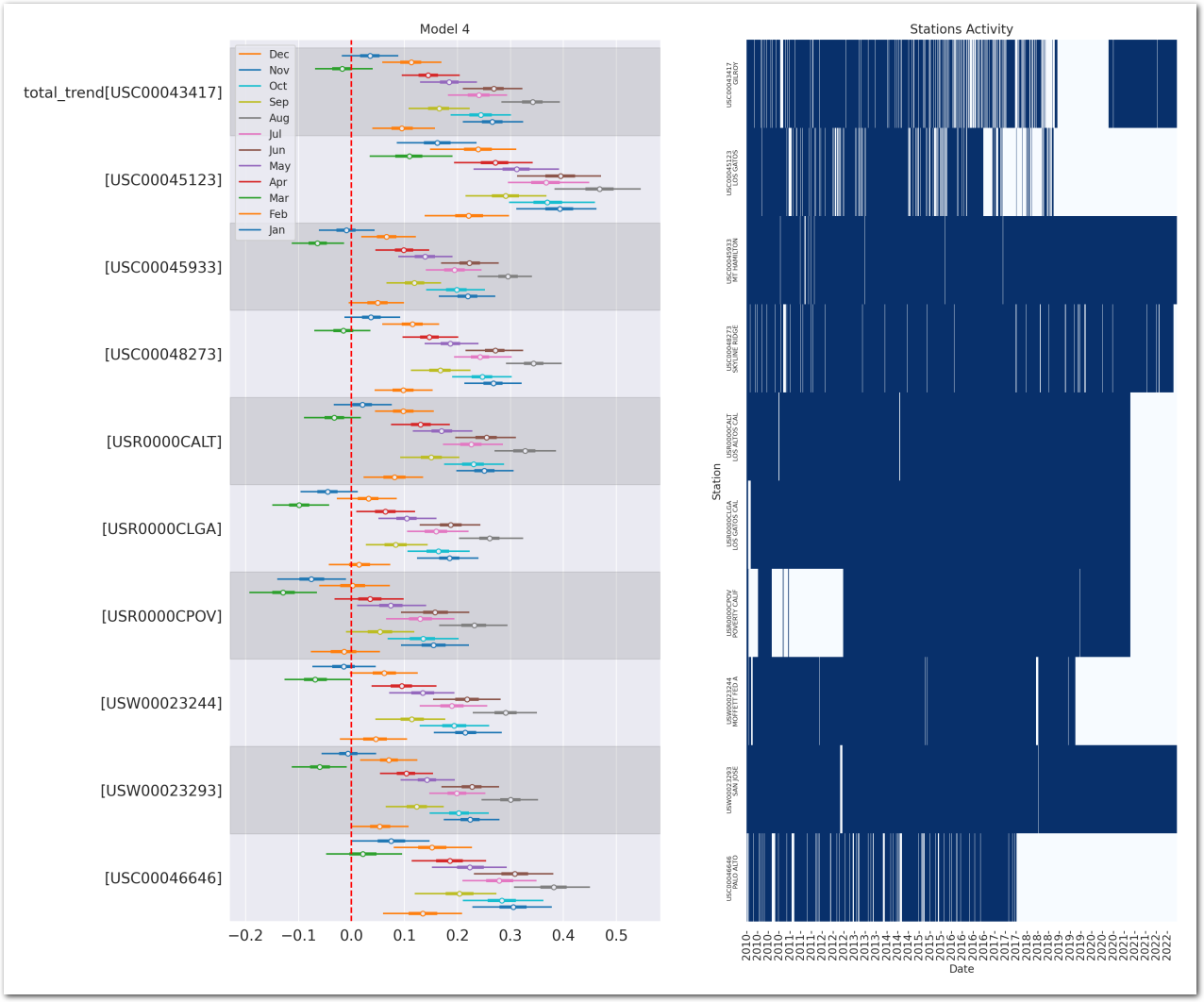
# dataframe with mean and CI for trend_sum
def summarize_model_with_month(idata, counties_stations_df, model_name):
idata_df = idata.posterior['total_trend'].mean(dim=['chain', 'draw']).to_dataframe().reset_index().rename(columns={'total_trend': 'mean'})
idata_df_ci = az.hdi(idata.posterior['total_trend'], hdi_prob=0.95).to_dataframe().reset_index()\
.pivot(index=['station', 'month'], columns='hdi', values='total_trend')\
.rename(columns={'lower': 'q_0.025', 'higher': 'q_0.975'})
idata_df = idata_df.merge(idata_df_ci, left_on=['station', 'month'], right_index=True)
# merge with counties_stations_df
idata_df = idata_df.merge(counties_stations_df.to_pandas()[['station', 'latitude', 'longitude', 'name', 'min_date', 'max_date']], left_on='station', right_on='station')
idata_df['model'] = model_name
return idata_df
idata4_df = summarize_model_with_month(idata_4, counties_stations_df, model_name='model_4')# plot the posterior trend_offset
fig, ax = plt.subplots(figsize=(10, 5))
# line plot with error bar with matplotlib and idata4_df
for station in idata4_df['station'].unique():
color = station_cmap[station]
# filter the dataframe for the station
idata_4_total_trend_ = idata4_df[idata4_df['station'] == station]
# plot the mean
ax.plot(idata_4_total_trend_['month'], idata_4_total_trend_['mean'], color=color, linewidth=1, label=station)
# plot the 95%-CI
ax.fill_between(idata_4_total_trend_['month'], idata_4_total_trend_['q_0.025'], idata_4_total_trend_['q_0.975'], color=color, alpha=0.1, linewidth=0.5)
# y axis label
ax.set_ylabel('Total trend [C/year]')
plt.title('Model 4: Total trend (trend + trend_offset_station + trend_offset_month) - mean and 95%-CI)')
# legend on the right
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0., ncol=2)
# horizontal red line at 0
plt.axhline(y=0, color='red', linestyle='--')
plt.show()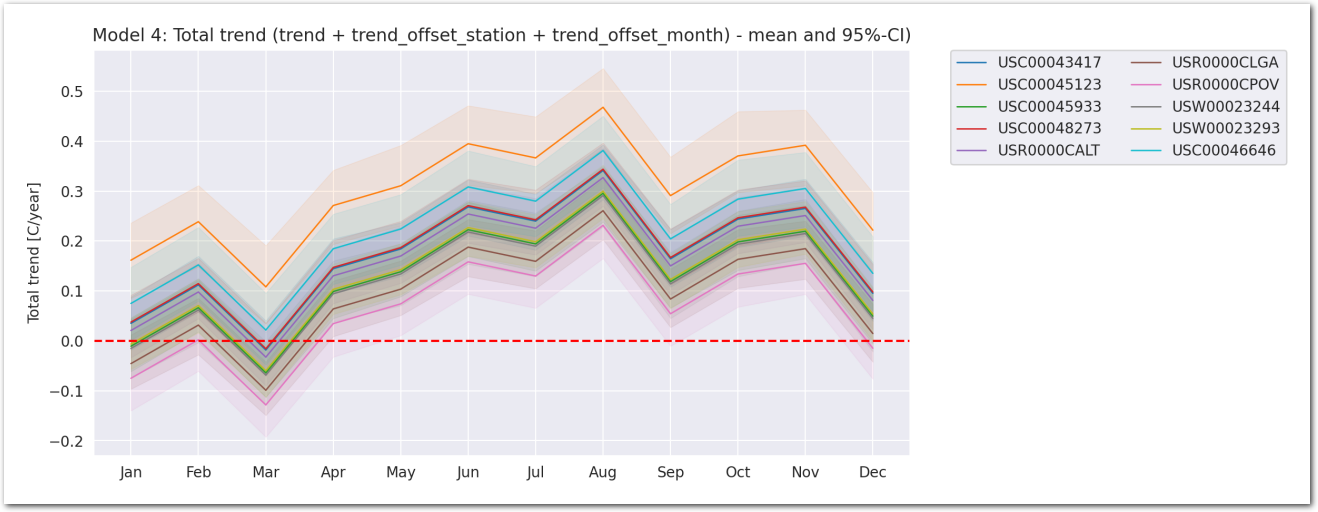
months = ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec']
total_trend_df = idata_4.posterior['total_trend'].mean(dim=['chain', 'draw']).to_dataframe().reset_index().rename(columns={'total_trend': 'mean'}).pivot(index='station', columns='month', values='mean')
# sort columns by month
total_trend_df = total_trend_df[months]
# heatmap with seaborn
n_stations = len(total_trend_df.index)
fig, ax = plt.subplots(figsize=(10, n_stations))
sns.heatmap(total_trend_df, ax=ax, cmap='RdBu_r', center=0, annot=True, fmt='.3f', linewidths=.5)
# y axis tickslabel with station names
ax.set_yticklabels(total_trend_df.index.map(lambda x: f"{x}\n{stations_df.row(by_predicate=(pl.col('station') == x), named=True)['name']}"))
# colorbar legend
ax.collections[0].colorbar.set_label("Total trend [C/year]")
plt.title('Model 4: Total trend (trend + trend_offset_station + trend_offset_month) - mean')
plt.show()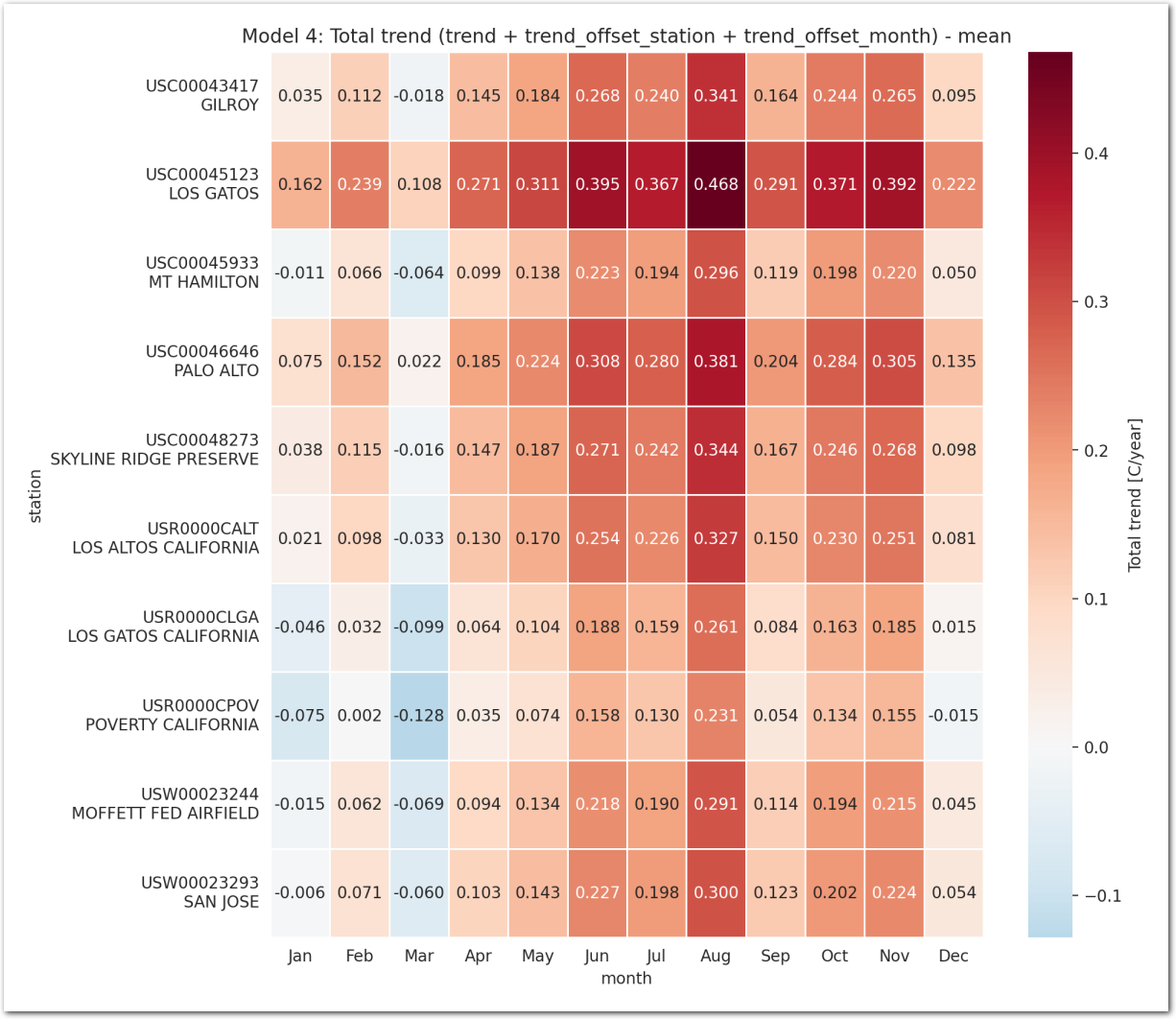
idata_4.posterior['total_trend'].quantile(0.025, dim=['chain', 'draw']).mean(dim=['month'])<xarray.DataArray 'total_trend' (station: 10)>
array([ 0.11621959, 0.22026046, 0.07460878, 0.12167755, 0.10206478,
0.0350285 , -0.00237606, 0.05889091, 0.07781911, 0.13952961])
Coordinates:
* station (station) <U11 'USC00043417' 'USC00045123' ... 'USC00046646'
quantile float64 0.025
idata_4.posterior['total_trend'].mean(dim=['chain', 'draw']).mean(dim=['month'])<xarray.DataArray 'total_trend' (station: 10)>
array([0.17303026, 0.29958936, 0.1273042 , 0.17555901, 0.15874312,
0.0923985 , 0.06293675, 0.12272283, 0.13153532, 0.21296856])
Coordinates:
* station (station) <U11 'USC00043417' 'USC00045123' ... 'USC00046646'
g = plot_posterior_predictive_model_alt(wx_pd, idata_4, stations_df, station_cmap, sample_posterior_predictive=sample_posterior_predictive)
plt.show()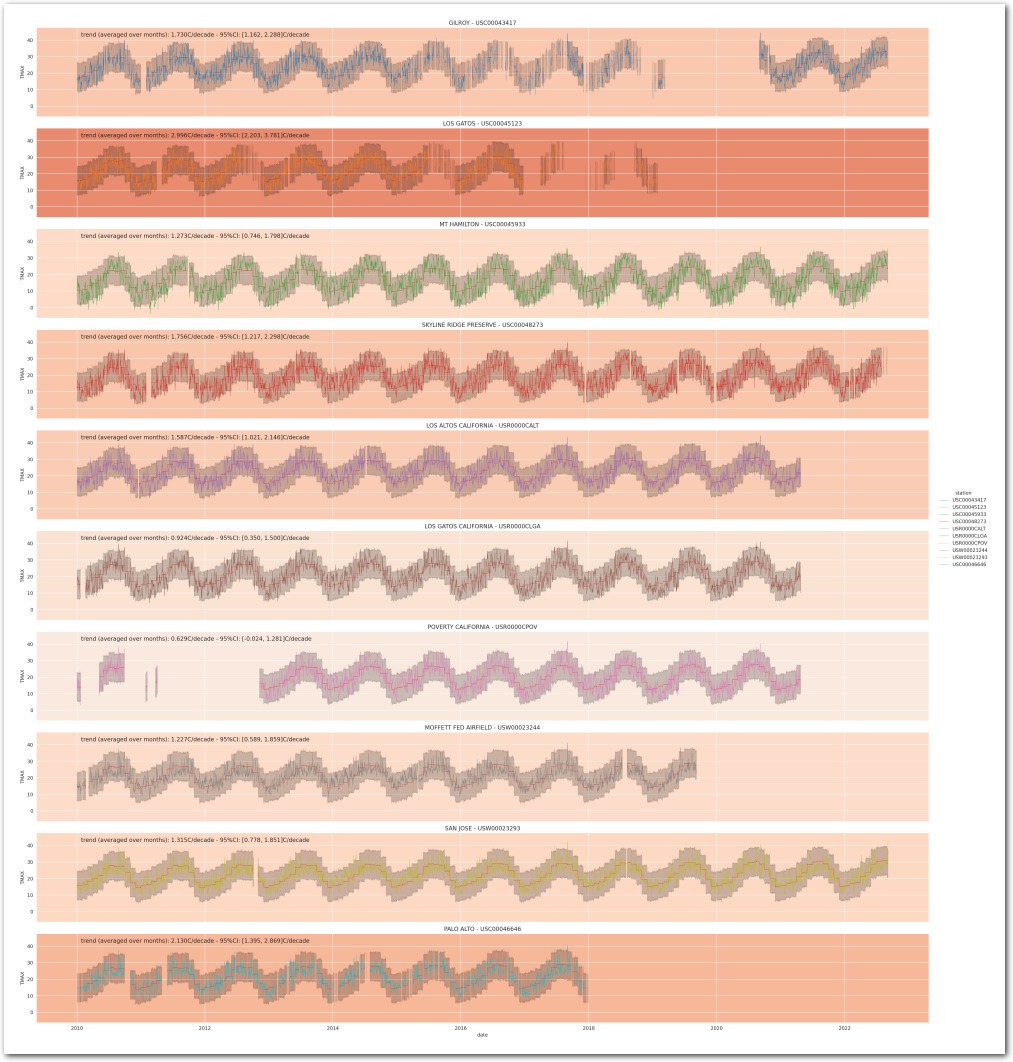
# average over months
idata4_df_ = idata4_df.groupby(['station', 'latitude', 'longitude', 'name', 'min_date', 'max_date', 'model']).agg({
'mean': 'mean',
'q_0.025': 'mean',
'q_0.975': 'mean',}).reset_index()
# plot map with the mean trend_station
us_map = pa.plot_county_geojson(geojson, counties,
zoom_start=8,
markers_fn=lambda m: trend_station_marker(m, idata_df=idata4_df_))
us_mapModel_5: With common, per month and station trends and per station as well as per month and per station offsets
In this model, the total trend is the sum of a common ‘trend’ and ‘trend_offset’ which is both per month and per station.
The temperature is linearly dependent on the time (year) through the total trend of the station with a per month offset and a per station offset.
We have: \[ TMAX_{i,j} \sim \mathcal{N}(\beta + \beta_{month_{j}} + \beta_{station_{i}} + (\gamma + \gamma_{station_{i}, month_{j}}) \times year_{j}, \sigma^2) \]
where:
- \(TMAX_{i,j}\) is the maximum temperature measured at station \(i\) at time \(j\)
- \(year_{j}\) is the time in years since Epoch 0 (1970-01-01 00:00:00 UTC)
- \(month_{j}\) is the month of the time of the measure
- \(\beta\) is the average temperature
- \(\beta_{month_{j}}\) is the offset of the temperature for each month with \(\beta_{month_{j}} \sim \mathcal{N}(\mu_{month}, \sigma_{month}^2)\) and the constraint that \(\sum_{j=1}^{12} \beta_{month_{j}} = 0\)
- \(\beta_{station_{i}}\) is the offset of the temperature for each station with \(\beta_{station_{i}} \sim \mathcal{N}(\mu_{station}, \sigma_{station}^2)\) and the constraint that \(\sum_{i=1}^{N} \beta_{station_{i}} = 0\)
- \(\gamma\) is the common slope of the linear relationship between the temperature and the time
- \(\gamma_{station_{i}, month_{j}}\) is the slope of the linear relationship between the temperature and the time for each station and each month with \(\gamma_{station_{i}, month_{j}} \sim \mathcal{N}(\mathbf{0}, (\sigma^{\gamma}_{station, month})^2)\)
def build_5(stations, wx_pd, time_idxs, times_f, station_idxs):
coords={
"station": stations,
"month": ["Jan", "Feb", "Mar", "Apr", "May", "Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec"],
"obs_id":[f'{loc}_{time.year}_{time.month}_{time.day}' for time, loc in wx_pd.index.values]
}
with pm.Model(coords=coords) as model:
t_ = pm.ConstantData('t', times_f)
month = pm.ConstantData('month', wx_pd['month'].values, dims=['obs_id'])
temp = pm.ConstantData('temp', wx_pd['TMAX'].values, dims=['obs_id'])
# priors
average_temperature = pm.Normal("average_temperature", 20, 10)
month_offset = pm.ZeroSumNormal("month_offset", sigma=5, dims="month")
trend = pm.Normal("trend", 0, 1)
trend_offset_sigma = pm.HalfNormal("trend_offset_sigma", 1)
trend_offset = pm.Normal("trend_offset", mu=0, sigma=trend_offset_sigma, dims=["station", "month"])
station_offset = pm.ZeroSumNormal("station_offset", sigma=3.0, dims="station")
expected_temperature = pm.Deterministic(
"expected_temperature",
average_temperature +
month_offset[month - 1] +
((trend + trend_offset[station_idxs, month - 1]) * t_[time_idxs]) +
station_offset[station_idxs],
dims=("obs_id")
)
sigma = pm.HalfNormal("sigma", 5)
# likelihood
pm.Normal("temperature", mu=expected_temperature, sigma=sigma, observed=temp, dims=("obs_id"))
return model
pm.model_to_graphviz(build_5(stations, wx_pd, time_idxs, times_f, station_idxs))
def build_and_sample(stations, wx_pd, time_idxs, times_f, station_idxs,
compute_convergence_checks=True,
sample_posterior_predictive=True,
compute_log_likelihood=True, nuts_sampler='pymc'):
model = build_5(stations, wx_pd, time_idxs, times_f, station_idxs)
idata = sample(model,
compute_convergence_checks=compute_convergence_checks,
sample_posterior_predictive=sample_posterior_predictive,
compute_log_likelihood=compute_log_likelihood,
nuts_sampler=nuts_sampler)
return idata
idata_5 = run_model(build_and_sample, stations, wx_pd, time_idxs, times_f, station_idxs,
compute_convergence_checks=compute_convergence_checks,
sample_posterior_predictive=sample_posterior_predictive,
compute_log_likelihood=compute_log_likelihood,
nuts_sampler=nuts_sampler)
idata_5Sampling 500 draws, 1000 tune, 4 chains, 4 cores
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [average_temperature, month_offset, trend, trend_offset_sigma, trend_offset, station_offset, sigma]100.00% [6000/6000 11:54<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 1_000 tune and 500 draw iterations (4_000 + 2_000 draws total) took 715 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters. A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
Sampling posterior predictive
Sampling: [temperature]100.00% [2000/2000 00:01<00:00]
Computing log likelihood100.00% [2000/2000 00:01<00:00]
Posterior predictive checks:
plot_ppc(idata_5)
plt.show()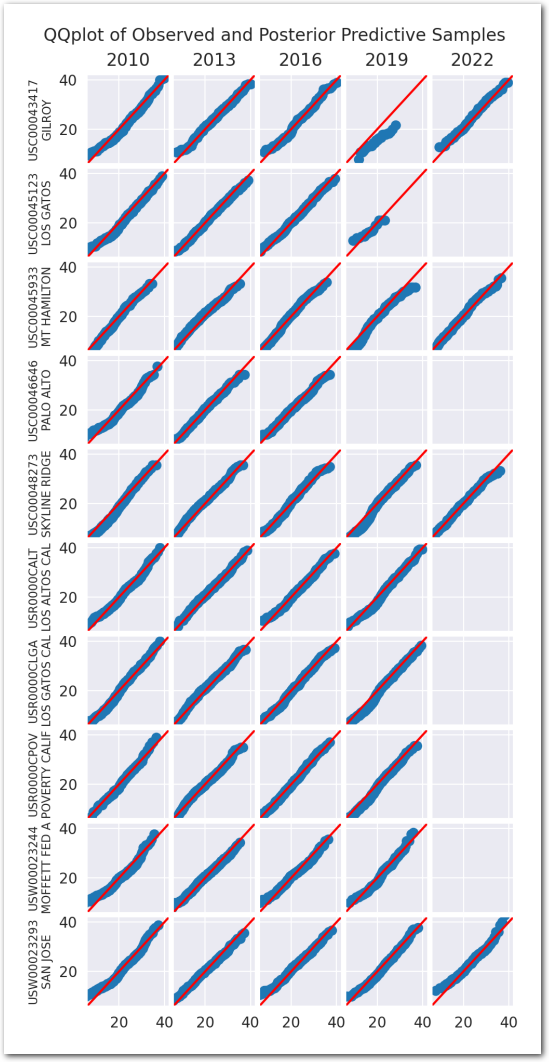
Posteriors:
az.summary(idata_5,
var_names=['average_temperature', 'trend', 'trend_offset', 'sigma', 'month_offset', 'station_offset'],
round_to=3, kind='stats')| mean | sd | hdi_3% | hdi_97% | |
|---|---|---|---|---|
| average_temperature | 14.557 | 0.311 | 14.006 | 15.165 |
| trend | 0.144 | 0.007 | 0.132 | 0.158 |
| trend_offset[USC00043417, Jan] | -0.025 | 0.012 | -0.047 | -0.001 |
| trend_offset[USC00043417, Feb] | -0.001 | 0.011 | -0.022 | 0.020 |
| trend_offset[USC00043417, Mar] | -0.004 | 0.011 | -0.024 | 0.018 |
| … | … | … | … | … |
| station_offset[USR0000CLGA] | 0.448 | 0.321 | -0.167 | 1.062 |
| station_offset[USR0000CPOV] | -0.957 | 0.335 | -1.547 | -0.304 |
| station_offset[USW00023244] | 0.142 | 0.321 | -0.491 | 0.713 |
| station_offset[USW00023293] | 0.998 | 0.302 | 0.401 | 1.544 |
| station_offset[USC00046646] | 0.087 | 0.342 | -0.524 | 0.722 |
145 rows × 4 columns
plot_summary(idata_5,
var_names=['average_temperature', 'trend', 'trend_offset', 'sigma', 'month_offset', 'station_offset'],
var_posteriors=['trend', 'trend_offset'],
var_ppcs=['temperature'],
sample_posterior_predictive=sample_posterior_predictive)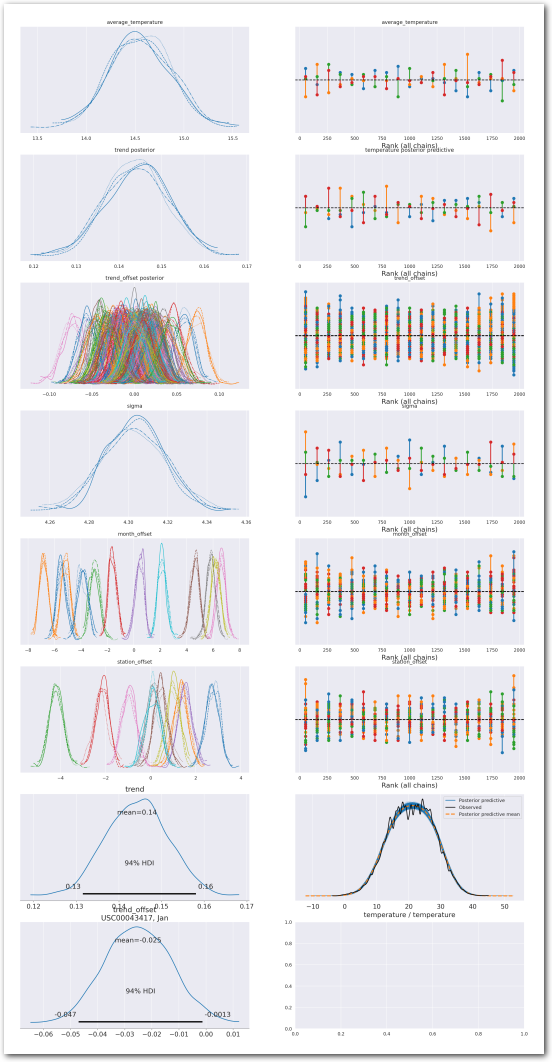
az.plot_forest(idata_5, var_names=keep_vars(idata_5),
combined=True, kind='forestplot', hdi_prob=0.95, figsize=(10, 10))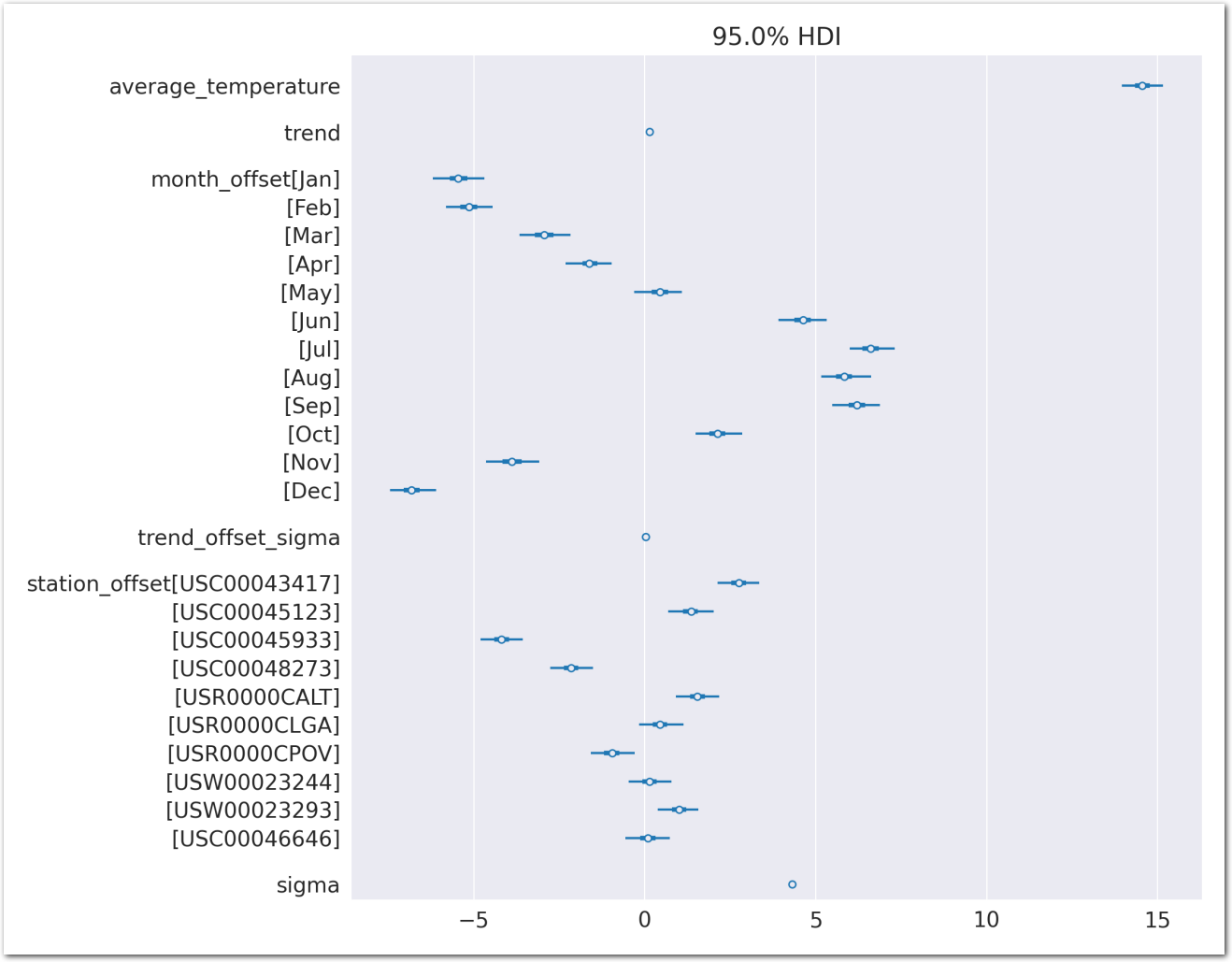
idata_5.posterior['total_trend'] = idata_5.posterior['trend'] + idata_5.posterior['trend_offset']plot_forest_trend_station_month(idata_5, counties_stations_heatmap, stations_df, title="Model 5")
plt.show()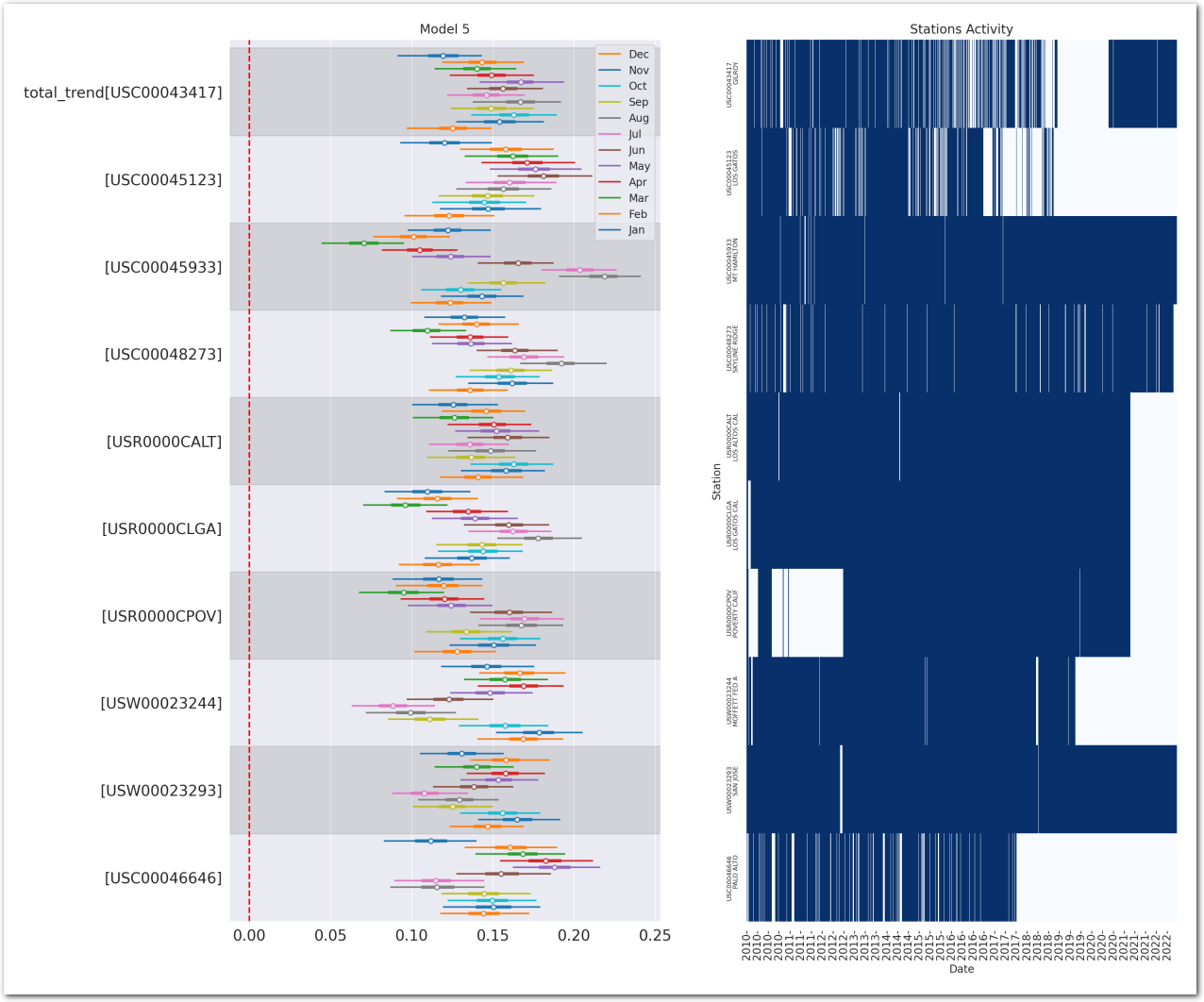
idata5_df = summarize_model_with_month(idata_5, counties_stations_df, model_name='model_5')# plot the posterior trend_offset
fig, ax = plt.subplots(figsize=(10, 5))
# line plot with error bar with matplotlib and idata5_df
for station in idata5_df['station'].unique():
color = station_cmap[station]
# filter the dataframe for the station
idata_5_total_trend_ = idata5_df[idata5_df['station'] == station]
# plot the mean
ax.plot(idata_5_total_trend_['month'], idata_5_total_trend_['mean'], color=color, linewidth=1, label=station)
# plot the 95%-CI
ax.fill_between(idata_5_total_trend_['month'], idata_5_total_trend_['q_0.025'], idata_5_total_trend_['q_0.975'], color=color, alpha=0.1, linewidth=0.5)
# y axis label
ax.set_ylabel('Total trend [C/year]')
plt.title('Model 5: Total trend (trend + trend_offset) - mean and 95%-CI)')
# legend on the right
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0., ncol=2)
# horizontal red line at 0
plt.axhline(y=0, color='red', linestyle='--')
plt.show()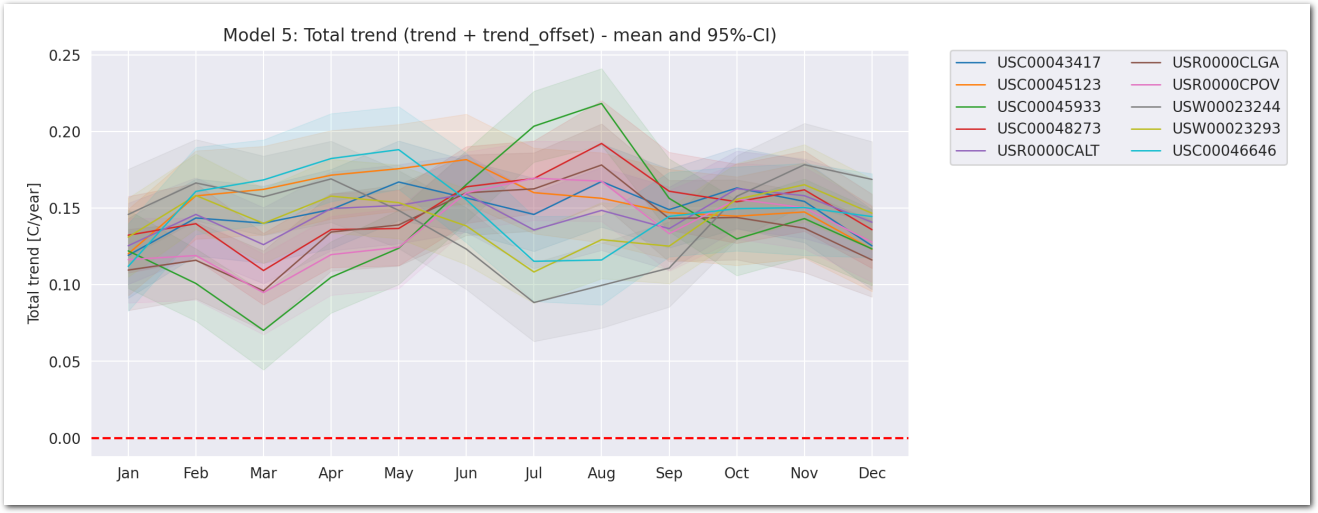
months = ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec']
total_trend_df = idata_5.posterior['total_trend'].mean(dim=['chain', 'draw']).to_dataframe().reset_index().rename(columns={'total_trend': 'mean'}).pivot(index='station', columns='month', values='mean')
# sort columns by month
total_trend_df = total_trend_df[months]
# heatmap with seaborn
n_stations = len(total_trend_df.index)
fig, ax = plt.subplots(figsize=(10, n_stations))
sns.heatmap(total_trend_df, ax=ax, cmap='RdBu_r', center=0, annot=True, fmt='.3f', linewidths=.5)
# y axis tickslabel with station names
ax.set_yticklabels(total_trend_df.index.map(lambda x: f"{x}\n{stations_df.row(by_predicate=(pl.col('station') == x), named=True)['name']}"))
# colorbar legend
ax.collections[0].colorbar.set_label("Total trend [C/year]")
plt.title('Model 5: Total trend (trend + trend_offset) - mean')
plt.show()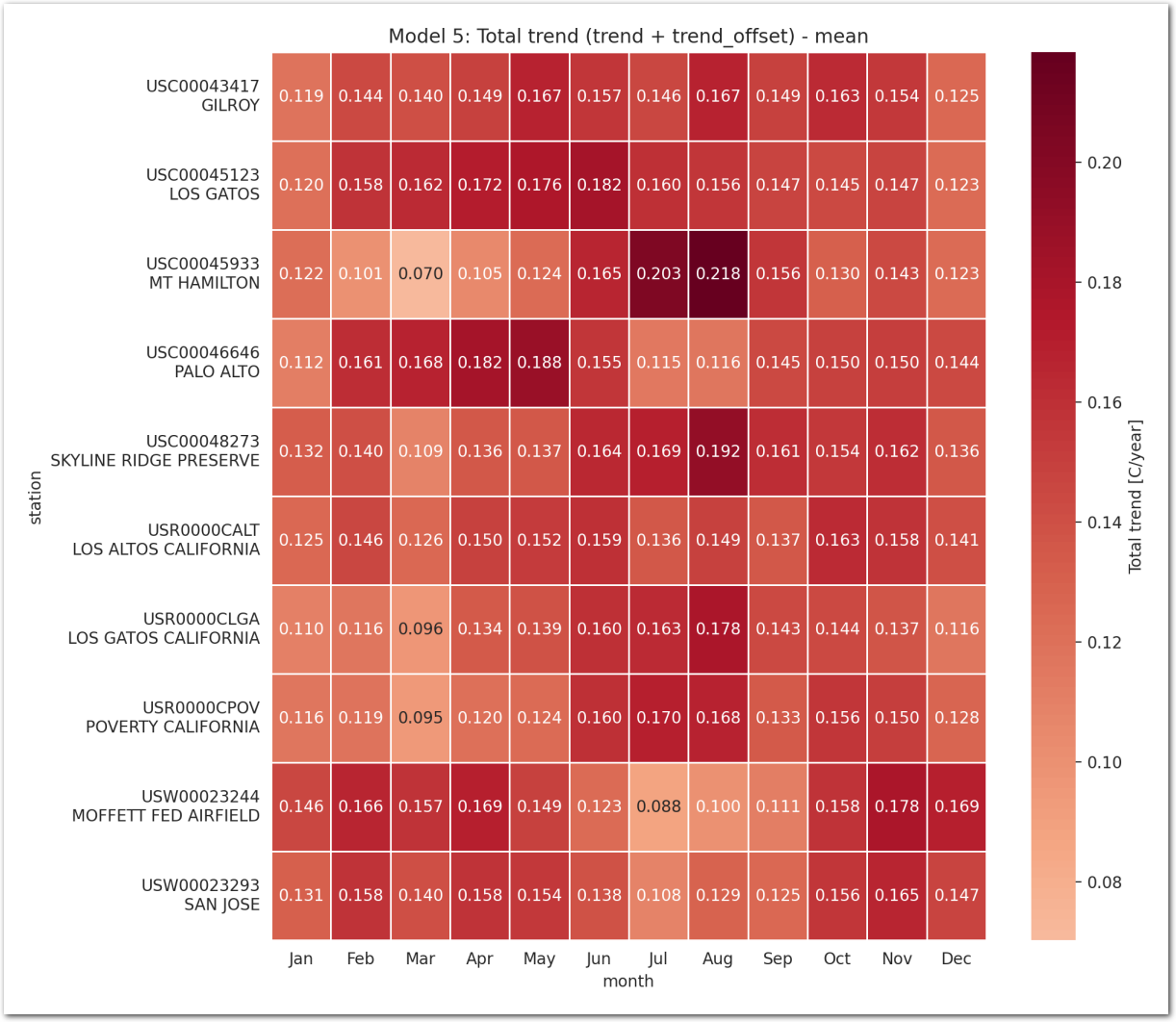
idata_5.posterior['total_trend'].quantile(0.025, dim=['chain', 'draw']).mean(dim=['month'])<xarray.DataArray 'total_trend' (station: 10)>
array([0.12283087, 0.12554789, 0.11335224, 0.1246666 , 0.1186764 ,
0.1100569 , 0.10979557, 0.11591885, 0.11796319, 0.12071353])
Coordinates:
* station (station) <U11 'USC00043417' 'USC00045123' ... 'USC00046646'
quantile float64 0.025
idata_5.posterior['total_trend'].mean(dim=['chain', 'draw']).mean(dim=['month'])<xarray.DataArray 'total_trend' (station: 10)>
array([0.1484043 , 0.15401381, 0.13847491, 0.14937379, 0.14505174,
0.13631847, 0.13655293, 0.14283405, 0.14247925, 0.148978 ])
Coordinates:
* station (station) <U11 'USC00043417' 'USC00045123' ... 'USC00046646'
g = plot_posterior_predictive_model_alt(wx_pd, idata_5, stations_df, station_cmap, sample_posterior_predictive=sample_posterior_predictive)
plt.show()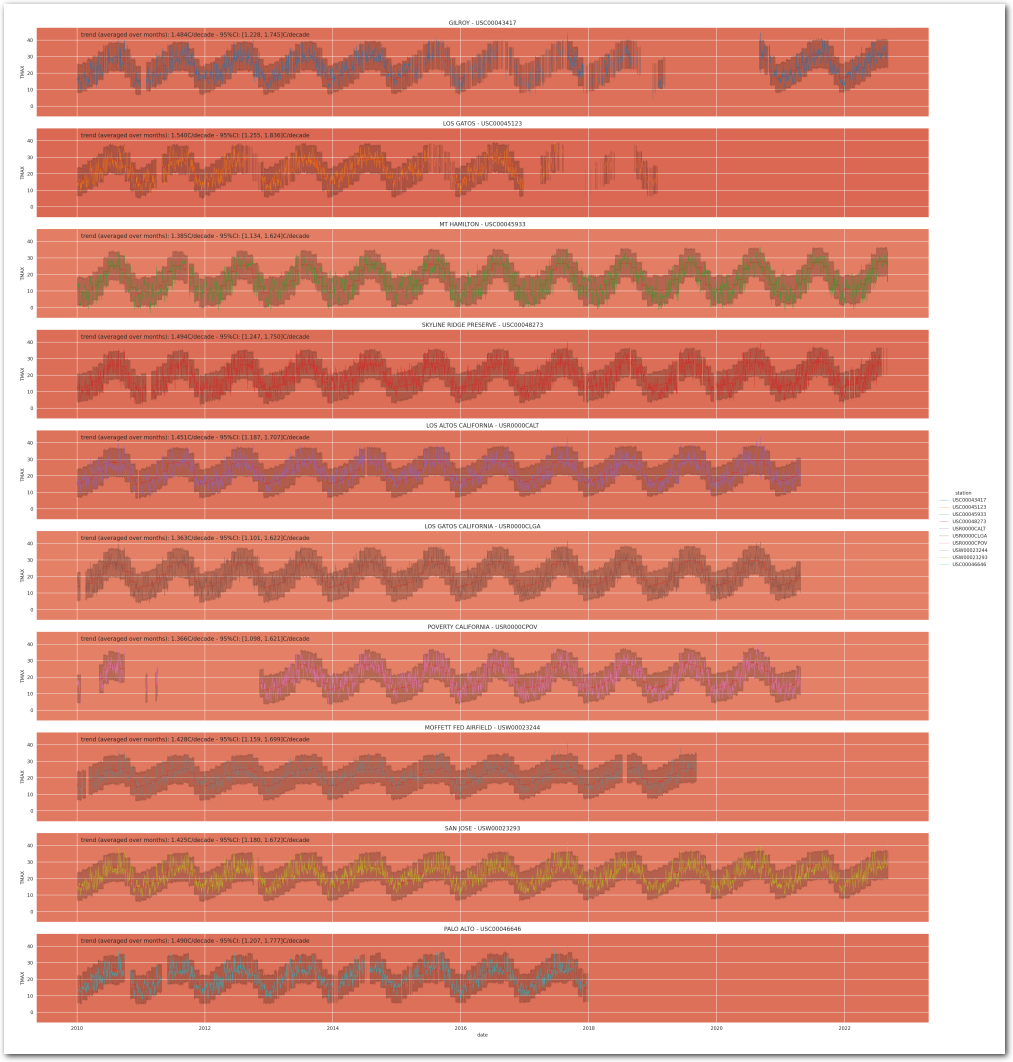
# average over months
idata5_df_ = idata5_df.groupby(['station', 'latitude', 'longitude', 'name', 'min_date', 'max_date', 'model']).agg({
'mean': 'mean',
'q_0.025': 'mean',
'q_0.975': 'mean',}).reset_index()
# plot map with the mean trend_station
us_map = pa.plot_county_geojson(geojson, counties,
zoom_start=8,
markers_fn=lambda m: trend_station_marker(m, idata_df=idata5_df_))
us_mapModel comparison
Comparison of trends in TMAX
az.plot_forest([idata_0, idata_1, idata_2, idata_3, idata_4, idata_5],
model_names=['model_0', 'model_1', 'model_2', 'model_3', 'model_4', 'model_5'],
var_names=['^trend'],
filter_vars='regex',
combined=True,
kind='forestplot',
hdi_prob=0.95,
figsize=(5, 40))
# vertical dash red line at 0
plt.axvline(x=0, color='red', linestyle='--')
plt.title(f'Model Comparison - TMAX trend (C/year) since {start_year}')
plt.show()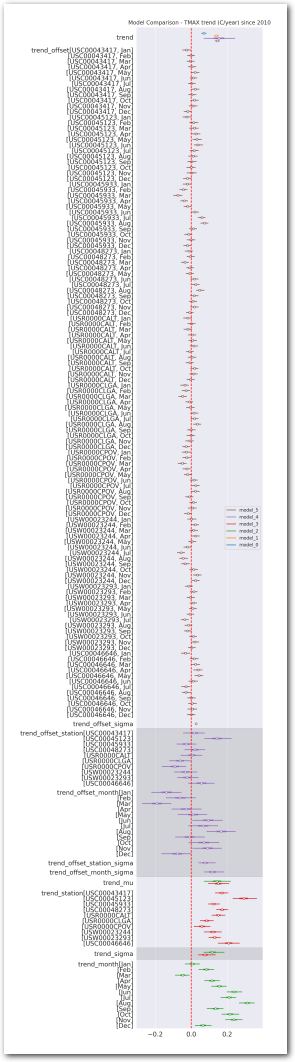
Comparison of models on ELPD
if compute_log_likelihood:
try:
df_comp = az.compare({'model_0': idata_0, 'model_1': idata_1, 'model_2': idata_2, 'model_3': idata_3, 'model_4': idata_4, 'model_5': idata_5}, ic='loo')
display(df_comp)
az.plot_compare(df_comp, insample_dev=False)
plt.show()
except Exception as e:
print(e)
else:
print('No log likelihood computed')| rank | elpd_loo | p_loo | elpd_diff | weight | se | dse | warning | scale | |
|---|---|---|---|---|---|---|---|---|---|
| model_5 | 0 | -106094.252273 | 117.609015 | 0.000000 | 9.684358e-01 | 136.898489 | 0.000000 | False | log |
| model_4 | 1 | -106848.964999 | 40.230693 | 754.712726 | 3.355445e-09 | 133.273687 | 40.060160 | False | log |
| model_2 | 2 | -106876.678132 | 33.466613 | 782.425859 | 3.677006e-09 | 133.224633 | 39.616787 | False | log |
| model_3 | 3 | -106967.205627 | 29.982068 | 872.953354 | 4.344803e-09 | 132.743327 | 39.493737 | False | log |
| model_1 | 4 | -106993.223015 | 22.255140 | 898.970742 | 4.641825e-09 | 132.660934 | 39.072083 | False | log |
| model_0 | 5 | -110670.762315 | 14.376978 | 4576.510042 | 3.156419e-02 | 149.487312 | 97.375544 | False | log |
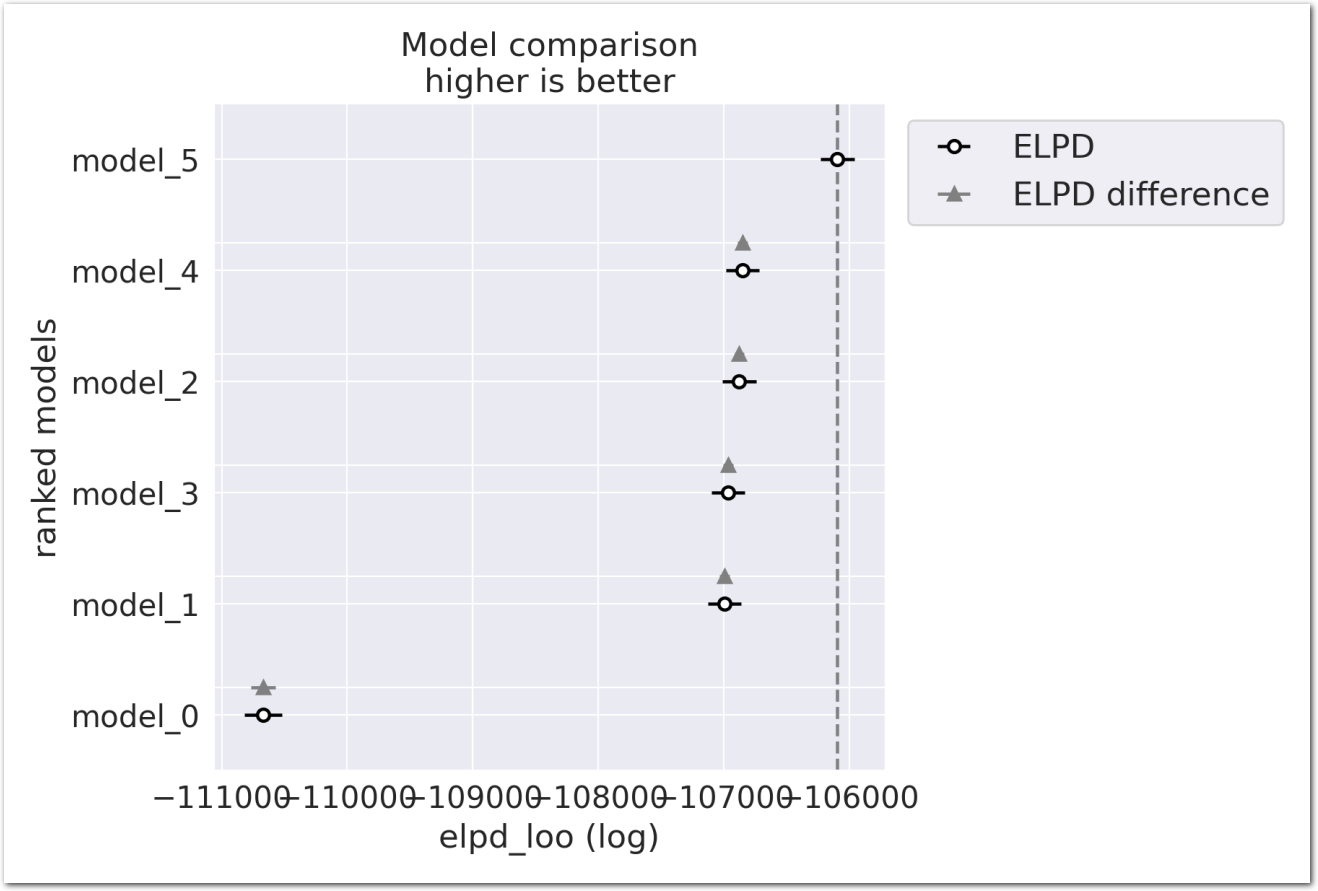
!dateMon Oct 30 18:17:38 UTC 2023Conclusion
I hope you like it hot! Let me know if you want the original notebook.
